题目内容
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间![]() 内)中,按照5%的比例进行分层抽样,统计结果按
内)中,按照5%的比例进行分层抽样,统计结果按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,整理如下图:
分组,整理如下图:
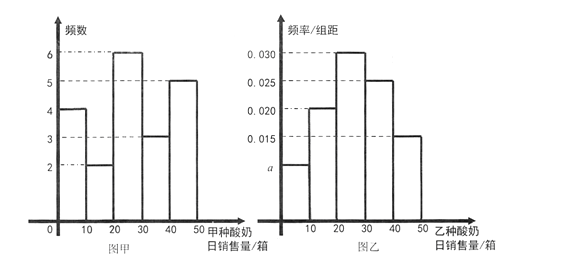
(Ⅰ)写出频率分布直方图(图乙)中![]() 的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为
的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为![]() ,
, ![]() ,试比较
,试比较![]() 与
与![]() 的大小(只需写出结论);
的大小(只需写出结论);
(Ⅱ)从甲种酸奶日销售量在区间![]() 的数据样本中抽取3个,记在
的数据样本中抽取3个,记在![]() 内的数据个数为
内的数据个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)估计1200个日销售量数据中,数据在区间![]() 中的个数.
中的个数.
【答案】(Ⅰ)![]() ,
, ![]() ;(Ⅱ)见解析;(Ⅲ)160个.
;(Ⅱ)见解析;(Ⅲ)160个.
【解析】试题分析:
(1)利用概率为1求得![]() 的值,然后比较
的值,然后比较![]() 的大小即可;
的大小即可;
(2)首先确定![]() 所有可能的取值,然后利用超几何分布概率公式求解概率,最后写出分布列即可即可
所有可能的取值,然后利用超几何分布概率公式求解概率,最后写出分布列即可即可
(3)分析所给数据,利用频率近似代替概率,然后利用古典概型相关结论即可求得最终结果.
试题解析:
(Ⅰ)由图(乙)知, ![]() 解得
解得![]() ,
, ![]() .
.
(Ⅱ)![]() 的所有可能取值1,2,3.
的所有可能取值1,2,3.
则![]() ,
, ![]() ,
, ![]() ,
,
其分布列如下:
| 1 | 2 | 3 |
|
|
|
|
(Ⅲ)由图(甲)知,甲种酸奶的数据共抽取![]() 个,
个,
其中有4个数据在区间![]() 内,
内,
又因为分层抽样共抽取了![]() 个数据,
个数据,
乙种酸奶的数据共抽取![]() 个,
个,
由(Ⅰ)知,乙种酸奶的日销售量数据在区间![]() 内的频率为0.1,
内的频率为0.1,
故乙种酸奶的日销售量数据在区间![]() 内有
内有![]() 个.
个.
故抽取的60个数据,共有![]() 个数据在区间
个数据在区间![]() 内.
内.
所以,在1200个数据中,在区间![]() 内的数据有160个.
内的数据有160个.

【题目】设某校新、老校区之间开车单程所需时间为![]() ,
, ![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.