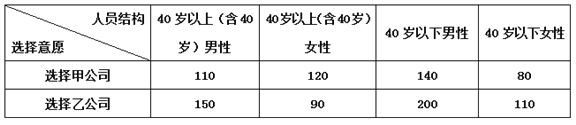
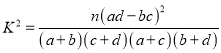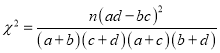题目内容
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.8元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.

(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
(ⅰ)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
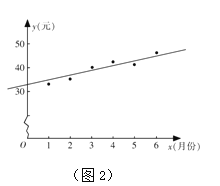
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
【答案】(Ⅰ)(ⅰ)![]() (ⅱ)
(ⅱ)![]() (Ⅱ)李某7月份的用水吨数约为13吨
(Ⅱ)李某7月份的用水吨数约为13吨
【解析】试题分析:
(i)由二项分布的概率公式可得概率为![]() ;
;
(ii)列出分布列,然后求得其属性期望值为![]() 吨;
吨;
(II)利用题意求得回归方程,然后结合题意可求得李某7月份的用水吨数为13吨.
试题解析:
解:(Ⅰ)(ⅰ)由题意,从全市居民中依次随机抽取5户,每户居民月用水量超过12吨的概率为![]() ,因此这5户居民恰好3户居民的月用水量都超过12吨的概率为
,因此这5户居民恰好3户居民的月用水量都超过12吨的概率为
![]() .
.
(ⅱ)由题设条件及月均用水量的频率分布直方图,可得居民每月的水费数据分组与概率分布表如下:
月用水量 |
|
|
|
价格 | 4 | 4.20 | 4.60 |
概率 | 0.9 | 0.06 | 0.04 |
所以全市居民用水价格的期望![]() 吨.
吨.
(Ⅱ)设李某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的对应点为
的对应点为![]() ,它们的平均值分别为
,它们的平均值分别为![]() ,则
,则![]() ,又点
,又点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,因此
,因此![]() ,所以7月份的水费为
,所以7月份的水费为![]() 元.
元.
设居民月用水量为![]() 吨,相应的水费为
吨,相应的水费为![]() 元,则
元,则
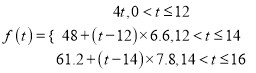 ,即:
,即:
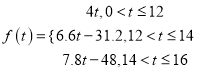
当![]() 时,
时, ![]() ,
,
所以李某7月份的用水吨数约为13吨.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案