题目内容
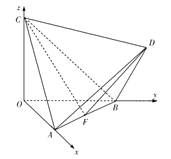
【题目】如下图,在空间直角坐标系![]() 中,正四面体(各条棱均相等的三棱锥)
中,正四面体(各条棱均相等的三棱锥)![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴上.
轴上.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)设![]() ,写出A,B,C的坐标,再求出D点坐标,从而得
,写出A,B,C的坐标,再求出D点坐标,从而得![]() 的坐标,只要它与平面
的坐标,只要它与平面![]() 的法向量垂直,即可证明线面平行;
的法向量垂直,即可证明线面平行;
(Ⅱ)求二面角,可取AB的中点F,由能证明∠CFD是所求二面角的平面角,在![]() 中由得余弦定理可得余弦值.也可求出二面角的两个面的法向量,由法向量夹角的余弦可得二面角的余弦.
中由得余弦定理可得余弦值.也可求出二面角的两个面的法向量,由法向量夹角的余弦可得二面角的余弦.
试题解析:
(Ⅰ)由![]() ,易知
,易知![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设![]() 点的坐标为
点的坐标为![]() ,则由
,则由![]() ,
,
可得![]()
![]() ,
,
解得![]() ,
,
所以![]() .
.
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,
则![]() ,
, ![]() ,
, ![]() 为二面角
为二面角![]() 的平面角.
的平面角.
由(Ⅰ)知,在![]() 中,
中, ![]() ,
, ![]() ,
,
则由余弦定理知![]() ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]() .
.

 名校练考卷期末冲刺卷系列答案
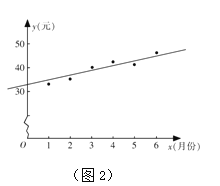
名校练考卷期末冲刺卷系列答案【题目】某购物网站对在7座城市的线下体验店的广告费指出![]() (万元)和销售额
(万元)和销售额![]() (万元)的数据统计如下表:
(万元)的数据统计如下表:
城市 |
|
|
|
|
|
|
|
广告费支出 |
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
(Ⅰ)若用线性回归模型拟合![]() 与
与![]() 关系,求
关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)若用对数函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程
的关系,可得回归方程![]() ,经计算对数函数回归模型的相关系数约为
,经计算对数函数回归模型的相关系数约为![]() ,请说明选择哪个回归模型更合适,并用此模型预测
,请说明选择哪个回归模型更合适,并用此模型预测![]() 城市的广告费用支出
城市的广告费用支出![]() 万元时的销售额.
万元时的销售额.
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, 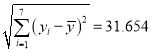 ,
, ![]() ,
, ![]() .
.
参考公式: 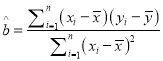 ,
, ![]() .
.
相关系数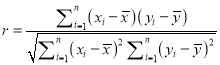 .
.
【题目】某次有600人参加的数学测试,其成绩的频数分布表如图所示,规定85分及其以上为优秀.
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 36 | 114 | 244 | 156 | 50 |
(Ⅰ)现用分层抽样的方法从这600人中抽取20人进行成绩分析,求其中成绩为优秀的学生人数;
(Ⅱ)在(Ⅰ)中抽取的20名学生中,要随机选取2名学生参加活动,记“其中成绩为优秀的人数”为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.