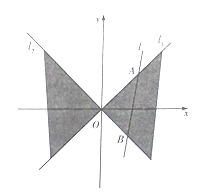
题目内容
【题目】已知经过![]() 两点的圆
两点的圆![]() 半径小于5,且在
半径小于5,且在![]() 轴上截得的线段长为
轴上截得的线段长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知直线![]() ,若
,若![]() 与圆
与圆![]() 交于
交于![]() 两点,且以线段
两点,且以线段![]() 为直径的圆经过坐标原点,求直线
为直径的圆经过坐标原点,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】试题分析:(1)设圆的一般方程为![]() ,因为直线过点
,因为直线过点![]() ,故
,故![]() ,又它截
,又它截![]() 轴所得的弦长为
轴所得的弦长为![]() ,故可得
,故可得![]() ,解方程组就可以得到
,解方程组就可以得到 ,从而圆的方程为
,从而圆的方程为![]() .(2)因为
.(2)因为![]() ,故设
,故设![]() ,再设
,再设![]() ,则以
,则以![]() 为直径的圆过原点可以转化为
为直径的圆过原点可以转化为![]() ,联立方程组消元后利用韦达定理把该关系式转化为关于
,联立方程组消元后利用韦达定理把该关系式转化为关于![]() 的方程即可解出
的方程即可解出![]() ,也就得到直线
,也就得到直线![]() 的方程.
的方程.
解析:(1)设圆的方程为![]() ,令
,令![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ① .又圆过
① .又圆过![]() 两点,故
两点,故![]() ,整理/span>
,整理/span>![]() ,消去
,消去![]() 得
得![]() ②,由①②得:
②,由①②得:  或
或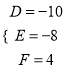 ,而圆的半径小于5,故
,而圆的半径小于5,故![]() ,故舍去
,故舍去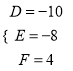 ,所以圆的方程为
,所以圆的方程为![]() .
.
(2)![]() ,设
,设![]() 的方程为:
的方程为: ![]() ,由
,由![]() ,消去
,消去![]() 得
得![]() .
.
设,则![]() .因为以
.因为以![]() 为直径的圆过原点,所以
为直径的圆过原点,所以![]() ,即
,即![]() ,故
,故![]() ,整理得:
,整理得: ![]() 或
或![]() ,当
,当![]() 或
或![]() 均满足
均满足![]() ,故
,故![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
相关题目