题目内容
已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值是( )
| A.-37 | B.-29 | C.-5 | D.以上都不对 |
A
f′(x)=6x2-12x=6x(x-2).
当-2<x<0时,f′(x)>0,∴f(x)在(-2,0)上为增函数;
当0<x<2时,f′(x)<0,∴f(x)在(0,2)上为减函数,
f(0)为极大值且f(0)=m,
∴f(x)max=m=3,此时f(2)=-5,f(-2)=-37.
∴f(x)在[-2,2]上的最小值为-37.
当-2<x<0时,f′(x)>0,∴f(x)在(-2,0)上为增函数;
当0<x<2时,f′(x)<0,∴f(x)在(0,2)上为减函数,
f(0)为极大值且f(0)=m,
∴f(x)max=m=3,此时f(2)=-5,f(-2)=-37.
∴f(x)在[-2,2]上的最小值为-37.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
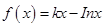 在区间
在区间 单调递增,则
单调递增,则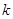 的取值范围是( )
的取值范围是( )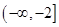
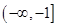
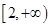

 ,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( ) 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是( )
的取值范围是( )



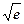 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。 ,其中
,其中 为自然对数的底数.
为自然对数的底数. 的单调区间;
的单调区间; 在点
在点 (其中
(其中 )处的切线为
)处的切线为 ,
, 轴、
轴、 轴所围成的三角形面积为
轴所围成的三角形面积为 ,求
,求
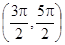


 的导函数为
的导函数为 ,若
,若 ,则
,则 .
.