题目内容

15．已知3x=5y，且$\frac{1}{x}$+$\frac{1}{y}$=3，则x+y=$\frac{1}{3}$（2+log35+log53）．

分析 根据指数幂和对数的关系进行化简即可．

解答 解：设3x=5y=t，则t＞0，
则x=log3t，y=log5t，
∵$\frac{1}{x}$+$\frac{1}{y}$=3，
∴$\frac{1}{lo{g}_{3}t}+\frac{1}{lo{g}_{5}t}$=3，
即logt3+logt5=logt15=3，
则t3=15，t=$\root{3}{15}$，
则x+y=log3t+log5t=log3$\root{3}{15}$+log5$\root{3}{15}$=$\frac{1}{3}$（log315+log515）=$\frac{1}{3}$（1+log35+1+log53）
=$\frac{1}{3}$（2+log35+log53），
故答案为：$\frac{1}{3}$（2+log35+log53）

点评 本题主要考查对数的化简，利用对数的换底公式进行化简是解决本题的关键．

练习册系列答案
相关题目
5．如图所示，已知|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=1，AB的中点是C，则$\overrightarrow{OC}$的坐标是（　　）
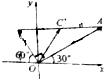
A．（$\frac{\sqrt{3}}{4}$-$\frac{1}{4}$，$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$）B．（$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$，$\frac{1}{2}$-$\frac{\sqrt{3}}{4}$）C．（$\frac{\sqrt{3}}{2}$-$\frac{1}{4}$，$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$）D．（$\frac{\sqrt{3}}{2}$-$\frac{1}{4}$，$\frac{\sqrt{3}}{4}$-$\frac{1}{2}$）
6．设$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$，且$\overrightarrow{a}$-$\overrightarrow{c}$与$\overrightarrow{b}$-$\overrightarrow{c}$的夹角为60°，则|$\overrightarrow{c}$|的最大值是2．
3．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，且|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{7}$．
（1）求$\overrightarrow{a}•\overrightarrow{b}$及$\overrightarrow{b}$在$\overrightarrow{a}$方向上的射影；
（2）求2$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$夹角θ的余弦值．
10．已知A={x|x2-8x+15=0}，B={x|x2-ax+2a+1=0}，B⊆A，求a的取值范围．
20．在△ABC中，tanA是以-4为3项，4为第5项的等差数列的公差，tanB是以$\frac{1}{3}$为第3项，9为第6项的等比数列的公比，则该三角形是（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形
7．已知一点在直线上从时刻t=0（s）开始以速度v（t）=t2-4t+3（m/s）运动，求：
（1）在t=4s时的位置；
（2）在t=4s的运动路程．
4．已知{an}为等差数列，{bn}为正项等比数列，公式q≠1，若a1=b1，a11=b11，则（　　）
A．a6＞b6或a6＜b6B．a6＜b6C．a6＞b6D．a6=b6
5．已知在数列{an}中，a1=1，a2=2，an+2=an+2n，则a10=42．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网