题目内容
6.已知点A(-1,0),B(0,1),点P是圆(x-a)2+y2=1上的动点,当数量积$\overrightarrow{AB}$•$\overrightarrow{AP}$取得最小值2时,点P的坐标为(1+$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).分析 设点P(a+cosθ,sinθ),求得$\overrightarrow{AB}$•$\overrightarrow{AP}$=a+cosθ+1+sinθ=a+1+$\sqrt{2}$cos(θ+$\frac{π}{4}$),再利用余弦函数的值域、$\overrightarrow{AB}$•$\overrightarrow{AP}$的最小值为2,求得a的值
解答 解:设点P(a+cosθ,sinθ),则由点A(-1,0),B(0,1),
可得$\overrightarrow{AB}$=(1,1),$\overrightarrow{AP}$=(a+cosθ+1,sinθ),
∴$\overrightarrow{AB}$•$\overrightarrow{AP}$=a+cosθ+1+sinθ=a+1+$\sqrt{2}$cos(θ+$\frac{π}{4}$),
故当cos(θ+$\frac{π}{4}$)=-1时,故数量积$\overrightarrow{AB}$•$\overrightarrow{AP}$的最小值为a+1-$\sqrt{2}$=2,∴a=1+$\sqrt{2}$,此时θ=$\frac{3π}{4}$;
故答案为:(1+$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$).
点评 本题主要考查两个向量的数量积公式,三角函数的恒等变换,余弦函数的值域,属于基础题

练习册系列答案
相关题目
17.正弦曲线y=sinx在点($\frac{π}{3}$,$\frac{\sqrt{3}}{2}$)的切线方程是( )
| A. | x+2y-$\sqrt{3}$+$\frac{π}{3}$=0 | B. | x-2y+$\sqrt{3}$-$\frac{π}{3}$=0 | C. | $\sqrt{3}$x-2y+$\sqrt{3}$-$\frac{\sqrt{3}}{3}$π=0 | D. | $\sqrt{3}$x+2y-$\sqrt{3}$+$\frac{\sqrt{3}}{3}$π=0 |
1.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y≤1}\\{x+y≥1}\\{y-2≤0}\end{array}\right.$,则目标函数z=3x+y的最大值为( )
| A. | -1 | B. | 3 | C. | 11 | D. | 12 |
11.已知i是虚数单位,a为实数,z为纯虚数,1+z=a+$\frac{1+i}{1-i}$,则z=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
18.5位男生与5位女生排成一排,男生甲与男生乙之间有且只有2位女生,女生不排在两端,这样的排列种数为( )
| A. | 5760 | B. | 57600 | C. | 2880 | D. | 28800 |
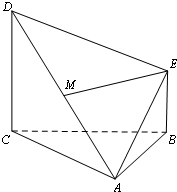 如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,
如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,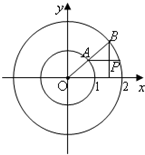 如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)
如图所示,射线OA与单位圆交于A,与圆x2+y2=4交于点B,过A平行于x轴的直线与过B与x轴垂直的直线交于P点,OA与x轴的夹角为x,若f(x)=$\overrightarrow{OA}$•$\overrightarrow{OP}$+cosx(cosx+2$\sqrt{3}$sinx)