题目内容
16.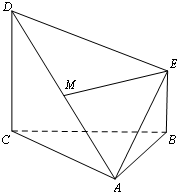 如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,
如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,点M为AD中点.
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求证:EM⊥平面ACD;
(Ⅲ)设P为线段BC上一点,且CP=2PB,试在线段AE上确定一点Q,使得
PQ∥平面ACD,并求出$\frac{EQ}{AE}$的值.
分析 (Ⅰ)设AC的中点为F,连结BF,MF.可证得四边形BEMF为平行四边形,进而ME∥BF,结合线面平行的判定定理,可得EM∥平面ABC;
(Ⅱ)在△ABC中,AB=BC,F为AC的中点,所以BF⊥AC,再由线面垂直的定义,结合CD⊥平面ABC,可得DC⊥BF,进而由线面垂直的判定定理,得到BF⊥平面ACD,结合线面垂直的第二判定定理得到EM⊥平面ACD;
(Ⅲ)过点P作PN∥AC交AB于N,过点N作QN∥BE交AE于Q,连结PQ,此时PQ∥平面ACD,由比例关系易得$EQ=\frac{1}{3}AE$.
解答 证明:(Ⅰ)设AC的中点为F,连结BF,MF.
在△ACD中,点M为AD中点,
$所以\;FM∥CD,FM=\frac{1}{2}CD$…(1分)
又因为CD⊥平面ABC,BE⊥平面ABC,
$所以\;BE∥CD,BE=\frac{1}{2}CD$,…(2分)
所以BE∥FM,BE=FM…(3分)
所以四边形BEMF为平行四边形.…(4分)
所以ME∥BF,ME?平面ABC,BF?平面ABC,
故EM∥平面ABC.…(5分)
(Ⅱ)在△ABC中,AB=BC,F为AC的中点,所以BF⊥AC.…(7分)
又因为CD⊥平面ABC,BF?平面ABC,
所以DC⊥BF.…(8分)
因为CD∩AC=C,
所以BF⊥平面ACD
由(Ⅰ)知 ME∥BF,
所以 EM⊥平面ADC.…(9分)
(Ⅲ)过点P作PN∥AC交AB于N,过点N作QN∥BE交AE于Q,
连结PQ,则由比例关系易得$EQ=\frac{1}{3}AE$.…(10分)
所以PN∥AC,PN?平面ACD,AC?平面ACD.…(11分)
所以PN∥平面ACD.
因为CD⊥平面ABC,BE⊥平面ABC,
所以CD∥BE.
$\begin{array}{l}故QN∥CD,\\ 又因为QN?平面ACD,CD?平面ACD,\end{array}$,…(12分)
由CD∩AC=C,CD,AC?平面ADC.
所以平面PQN∥平面ACD,
由PQ?平面PQN.
故PQ∥平面ACD.
$所以\frac{EQ}{AE}=\frac{1}{3}$.…(14分)
点评 本题考查的知识点是直线与平面平行的判定,直线平面垂直的判定,考查转化能力和空间想像能力,难度中档.

| 地区类别 | 首小时内 | 首小时外 |
| 一类 | 2.5元/15分钟 | 3.75元/15分钟 |
| 二类 | 1.5元/15分钟 | 2.25元/15分钟 |
| 三类 | 0.5元/15分钟 | 0.75元/15分钟 |
| A. | 一类 | B. | 二类 | C. | 三类 | D. | 无法判断 |
| A. | [$\frac{1}{2}$,$\frac{4}{3}$] | B. | [0,$\frac{1}{2}$] | C. | (-∞,0]∪[$\frac{4}{3}$,+∞) | D. | [0,$\frac{4}{3}$] |
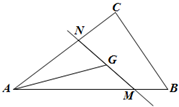 如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )
如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
| A. | {0,3,4,2} | B. | {0,2} | C. | {1,5} | D. | {2,0,1,5} |