题目内容
1．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y≤1}\\{x+y≥1}\\{y-2≤0}\end{array}\right.$，则目标函数z=3x+y的最大值为（ ）| A． | -1 | B． | 3 | C． | 11 | D． | 12 |
分析 作出不等式组对应的平面区域，利用目标函数的几何意义，求最大值．
解答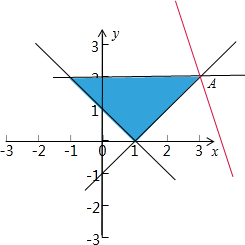 
解：作出不等式组$\left\{\begin{array}{l}x-y≤1\\ x+y≥1\\ y-2≤0\end{array}\right.$对应的平面区域如图：（阴影部分）．
由z=3x+y得y=-3x+z，
平移直线y=-3x+z，
由图象可知当直线y=-3x+z经过点A时，直线y=-3x+z的截距最大，
此时z最大．
由$\left\{\begin{array}{l}x-y=1\\ y-2=0\end{array}\right.$，解得$\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$，即A（3，2），
代入目标函数z=3x+y得z=3×3+2=11．
即目标函数z=3x+y的最大值为11．
故选：C．
点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
相关题目
11．已知直线y=kx+2与圆（x+2）2+（y-1）2=4相交于M，N两点，若|MN|≥2$\sqrt{3}$，则k的取值范围是（ ）
| A． | [$\frac{1}{2}$，$\frac{4}{3}$] | B． | [0，$\frac{1}{2}$] | C． | （-∞，0]∪[$\frac{4}{3}$，+∞） | D． | [0，$\frac{4}{3}$] |
如图，PA是圆的切线，A为切点，PBC是圆的割线，且PB=$\frac{1}{2}$BC，则$\frac{PA}{PB}$=$\sqrt{3}$．
9．“已知关于x的不等式ax2+bx+c＞0的解集为（1，2），解关于x的不等式cx2+bx+a＞0．”给出如下的一种解法：
解：由ax2+bx+c＞0的解集为（1，2），得，a（$\frac{1}{x}$）2+b（$\frac{1}{x}$）+c＞0的解集为（$\frac{1}{2}$，1），
即关于x的不等式cx2+bx+a＞0的解集为（$\frac{1}{2}$，1）．
参考上述解法：若关于x的不等式$\frac{b}{x+a}$+$\frac{x+b}{x+c}$＜0的解集为（-1，-$\frac{1}{3}$）∪（$\frac{1}{2}$，1），则关于x的不等式$\frac{b}{x-a}$-$\frac{x-b}{x-c}$＞0的解集为（ ）
解：由ax2+bx+c＞0的解集为（1，2），得，a（$\frac{1}{x}$）2+b（$\frac{1}{x}$）+c＞0的解集为（$\frac{1}{2}$，1），
即关于x的不等式cx2+bx+a＞0的解集为（$\frac{1}{2}$，1）．
参考上述解法：若关于x的不等式$\frac{b}{x+a}$+$\frac{x+b}{x+c}$＜0的解集为（-1，-$\frac{1}{3}$）∪（$\frac{1}{2}$，1），则关于x的不等式$\frac{b}{x-a}$-$\frac{x-b}{x-c}$＞0的解集为（ ）
| A． | （-1，1） | B． | （-1，-$\frac{1}{2}$）∪（$\frac{1}{3}$，1） | C． | （-∞，-$\frac{1}{2}$）∪（$\frac{1}{3}$，1） | D． | （-∞，-$\frac{1}{2}$）∪（$\frac{1}{3}$，+∞） |
13．已知命题p：函数y=f（x）在区间[a，b]上单调递增，命题q：函数y=f（x）单调递增区间为[a，b]，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
10．某篮球架的底座三视图如图所示，则其体积为（ ）
| A． | $\frac{{470+10\sqrt{30}}}{3}$ | B． | 175 | C． | 180 | D． | 295+10$\sqrt{2}$ |