题目内容
14．已知过点（1，1）的直线与圆x2+y2-4x-6y+4=0相交于A，B两点，则|AB|的最小值为4．分析 把圆的方程化为标准方程，求得圆心和半径，求得弦心距d的最大值，可得|AB|的最小值．
解答 解：圆x2+y2-4x-6y+4=0 即 （x-2）2+（y-3）2=9，表示以C（2，3）为圆心、半径等于3的圆，
要使弦长最小，只有弦心距最大．
而弦心距d的最大值为$\sqrt{（2-1）^{2}+（3-1）^{2}}$=$\sqrt{5}$，
∴|AB|的最小值为2$\sqrt{{r}^{2}-{d}^{2}}$=4，
故答案为：4．
点评 本题主要考查直线和圆的位置关系，两点间的距离公式，弦长公式的应用，属于中档题．
练习册系列答案
相关题目
4．为了缓解城市拥堵，某市对非居民区的公共停车场制定了不同的收费标准（见表）．
如果小王某次停车3小时，缴费24元，请你判断小王该次停车所在地区的类别是（ ）
| 地区类别 | 首小时内 | 首小时外 |
| 一类 | 2.5元/15分钟 | 3.75元/15分钟 |
| 二类 | 1.5元/15分钟 | 2.25元/15分钟 |
| 三类 | 0.5元/15分钟 | 0.75元/15分钟 |
| A． | 一类 | B． | 二类 | C． | 三类 | D． | 无法判断 |
2．江苏舜天足球俱乐部为救助在“3.10云南盈江地震”中失学的儿童，准备在江苏省五台山体育场举行多场足球义赛，预计卖出门票2.4万张，票价分别为3元、5元和8元三种，且票价3元和5元的张数的积为0.6万张．设x是门票的总收入，经预算扣除其它各项开支后，该俱乐部的纯收入函数模型为y=lg2x，则当这三种门票的张数分别为（ ）万张时，可以为失学儿童募捐的纯收入最大．
| A． | 1、0．、0.8 | B． | 0.6、0.8、1 | C． | 0.6、1、0.8 | D． | 0.6、0.6、0.8 |
9．“已知关于x的不等式ax2+bx+c＞0的解集为（1，2），解关于x的不等式cx2+bx+a＞0．”给出如下的一种解法：
解：由ax2+bx+c＞0的解集为（1，2），得，a（$\frac{1}{x}$）2+b（$\frac{1}{x}$）+c＞0的解集为（$\frac{1}{2}$，1），
即关于x的不等式cx2+bx+a＞0的解集为（$\frac{1}{2}$，1）．
参考上述解法：若关于x的不等式$\frac{b}{x+a}$+$\frac{x+b}{x+c}$＜0的解集为（-1，-$\frac{1}{3}$）∪（$\frac{1}{2}$，1），则关于x的不等式$\frac{b}{x-a}$-$\frac{x-b}{x-c}$＞0的解集为（ ）
解：由ax2+bx+c＞0的解集为（1，2），得，a（$\frac{1}{x}$）2+b（$\frac{1}{x}$）+c＞0的解集为（$\frac{1}{2}$，1），
即关于x的不等式cx2+bx+a＞0的解集为（$\frac{1}{2}$，1）．
参考上述解法：若关于x的不等式$\frac{b}{x+a}$+$\frac{x+b}{x+c}$＜0的解集为（-1，-$\frac{1}{3}$）∪（$\frac{1}{2}$，1），则关于x的不等式$\frac{b}{x-a}$-$\frac{x-b}{x-c}$＞0的解集为（ ）
| A． | （-1，1） | B． | （-1，-$\frac{1}{2}$）∪（$\frac{1}{3}$，1） | C． | （-∞，-$\frac{1}{2}$）∪（$\frac{1}{3}$，1） | D． | （-∞，-$\frac{1}{2}$）∪（$\frac{1}{3}$，+∞） |
19．
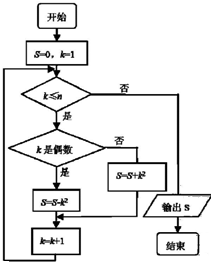阅读如图所示的程序框图，运行相应的程序，若输入n的值为100，则输出S的值为（ ）
阅读如图所示的程序框图，运行相应的程序，若输入n的值为100，则输出S的值为（ ）| A． | -1050 | B． | 5050 | C． | -5050 | D． | -4950 |