题目内容
19. 如图所示,已知圆O1与圆O2相交于A、B两点,过A点作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1、圆O2于点D、E,DE与AC相交于点P.
如图所示,已知圆O1与圆O2相交于A、B两点,过A点作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1、圆O2于点D、E,DE与AC相交于点P.(1)求证:AD∥EC;
(2)若PA=6,PC=2,BD=9,求PE的长.
分析 (1)连接AB,根据弦切角等于所夹弧所对的圆周角得到∠BAC=∠D,又根据同弧所对的圆周角相等得到∠BAC=∠E,等量代换得到∠D=∠E,根据内错角相等得到两直线平行即可;
(2)设BP=x,PE=y,根据相交弦定理得PA•PC=BP•PE,求出xy=12,再根据AD∥EC得$\frac{9x}{y}$=$\frac{6}{2}$,求出x,y,即可求出PE的长.
解答 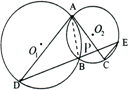 (1)证明:连接AB,
(1)证明:连接AB,
∵AC是⊙O1的切线,
∴∠BAC=∠D,
又∵∠BAC=∠E,
∴∠D=∠E,
∴AD∥EC.
(2)解:设BP=x,PE=y,
∵PA=6,PC=2,
∴xy=12①,
∵AD∥EC,
∴$\frac{DP}{PE}=\frac{AP}{PC}$,
∴$\frac{9x}{y}$=$\frac{6}{2}$②,
由①②可得x=3,y=4(负数舍去).
点评 此题是一道综合题,要求学生灵活运用直线与圆相切和相交时的性质解决实际问题.本题的突破点是辅助线的连接.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,求$\overrightarrow{AE}$•$\overrightarrow{AF}$.
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,求$\overrightarrow{AE}$•$\overrightarrow{AF}$.
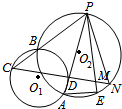 如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N.
如图,已知⊙O1与⊙O2相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N. 长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=BC=2,O是底面对角线的交点.
长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=BC=2,O是底面对角线的交点.