题目内容
4.已知函数f(x)=t($\frac{1}{x}$-1)+lnx,t为常数,且t>0.(1)若曲线y=f(x)上一点($\frac{1}{2}$,y0)处的切线方程为y+2x+ln2-2=0,求t和y0;
(2)若f(x)在区间[1,+∞)上是单调递增函数,求t的取值范围;
(3)当t=1时,证明:1-$\frac{1}{x}$≤lnx≤x-1.
分析 (1)首先求出函数的导数,然后根据条件列方程组$\left\{\begin{array}{l}{{y}_{0}+2×\frac{1}{2}+ln-2=0}\\{f′(\frac{1}{2})=-2}\end{array}\right.$,并解方程组即可求出结果;
(2)由f(x)在区间[1,+∞)上是单调递增函数⇒f'(x)≥0在x∈[1,+∝)上恒成立,然后分离参数t≤x恒成立,进而根据x≥1,求出t的范围.
(3)当t=1时,由函数f(x)在区间[1,+∞)上是单调递增函数,f(1)=0,可得f(x)≥0,即1-$\frac{1}{x}$≤lnx 成立.再根据m(x)=x-1-lnx在区间[1,+∞)上是单调递增函数,m(1)=0,可得m(x)≥0,即lnx≤x-1.综合即可证得结论.
解答 解:(1)∵函数f(x)=t($\frac{1}{x}$-1)+lnx,t为常数,且t>0,∴f'(x)=$\frac{x-t}{{x}^{2}}$(x>0).
由题意知$\left\{\begin{array}{l}{{y}_{0}+2×\frac{1}{2}+ln-2=0}\\{f′(\frac{1}{2})=-2}\end{array}\right.$,求得$\left\{\begin{array}{l}{t=1}\\{{y}_{0}=1-ln2}\end{array}\right.$.
(2)若f(x)在区间[1,+∞)上是单调递增函数,
则f'(x)≥0在x∈[1,+∝)上恒成立,即t≤x恒成立.
∵x≥1,∴t≤1.
又∵t>0,∴0<t≤1.
(3)当t=1时,∵函数f(x)=$\frac{1}{x}$-1+lnx在区间[1,+∞)上是单调递增函数,f(1)=0,
∴f(x)≥0,即1-$\frac{1}{x}$≤lnx 成立.
再根据m(x)=x-1-lnx在区间[1,+∞)上是单调递增函数,m(1)=0,∴m(x)≥0,
即lnx≤x-1.
综上可得,1-$\frac{1}{x}$≤lnx≤x-1.
点评 本题考查了利用导数研究函数的单调性,以及求切线方程,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于难题.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
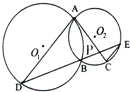 如图所示,已知圆O1与圆O2相交于A、B两点,过A点作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1、圆O2于点D、E,DE与AC相交于点P.
如图所示,已知圆O1与圆O2相交于A、B两点,过A点作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1、圆O2于点D、E,DE与AC相交于点P.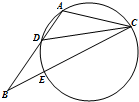 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC=6,EC=6,则AD的长为$\frac{3}{2}$.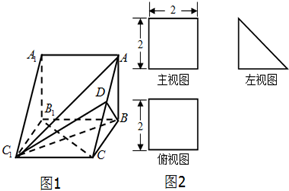 三棱柱A的直观图(图1)及三视图(图2)(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,A为A的中点.
三棱柱A的直观图(图1)及三视图(图2)(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,A为A的中点.