题目内容
已知数列{ }中,
}中,  ,
, ,
,
(1)求证数列{
 }为等比数列.
}为等比数列.
(2)判断265是否是数列{ }中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.
}中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.
 }中,
}中,  ,
, ,
,(1)求证数列{

 }为等比数列.
}为等比数列.(2)判断265是否是数列{
 }中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.
}中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.(1) 详见解析;(2) 265是数列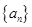 中的第9项。
中的第9项。
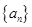 中的第9项。
中的第9项。试题分析:(1) 根据等比数列的定义证明
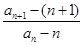 为常数即可。(2)由(1)可得数列
为常数即可。(2)由(1)可得数列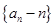 的通项公式,从而可得
的通项公式,从而可得 ,解
,解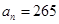 ,解得
,解得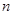 若为正整数,说明265是
若为正整数,说明265是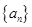 中的项;否则不是数列
中的项;否则不是数列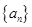 中的项。
中的项。(1)证明由
 知
知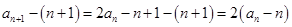
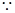
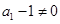
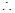
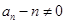
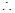

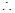 {
{
 }是以1为首项,以2为公比的等比数列. 6分
}是以1为首项,以2为公比的等比数列. 6分(2).由(1)知
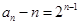 ,
,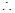
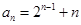 . 8分
. 8分265是数列
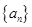 中的第9项.(原因是
中的第9项.(原因是 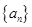 是递增数列,265是奇数,它只能为
是递增数列,265是奇数,它只能为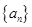 中的奇数项,又
中的奇数项,又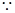 2
2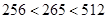
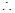 猜想是第9 项,经验证符合猜想,不写原因不扣分) 9分
猜想是第9 项,经验证符合猜想,不写原因不扣分) 9分
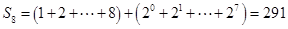 12分
12分
练习册系列答案
相关题目
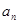 }中,
}中,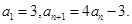
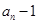 }是等比数列,并求出数列{
}是等比数列,并求出数列{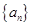 满足
满足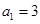 ,
,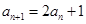 ,
,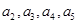 ;
; 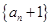 是等比数列;并求出
是等比数列;并求出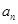 的表达式.
的表达式.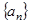 的前
的前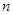 项和为
项和为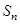 ,已知
,已知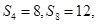 则
则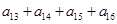 的值为 .
的值为 .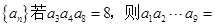 ________.
________. ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )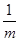 +
+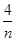 的最小值为( )
的最小值为( )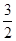
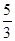
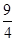
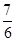
 ,若
,若 +
+ =20,
=20, +
+ =80,则
=80,则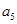 +
+ 等于( )
等于( )