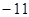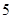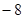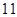题目内容
已知各项为正的等比数列{an}中,a4与a14的等比中项为 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )
 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )| A.16 | B.8 | C. | D.4 |
B
由题意知,a4·a14=8
∵数列{an}是等比数列
∴a7·a11=a4·a14=8
由均值定理得:2a7+a11≥2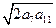 =2
=2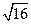 =8
=8
等号当且仅当2a7=a11,即a7=2,a11=4时成立
∵数列{an}是等比数列
∴a7·a11=a4·a14=8
由均值定理得:2a7+a11≥2
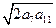 =2
=2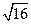 =8
=8等号当且仅当2a7=a11,即a7=2,a11=4时成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 }中,
}中,  ,
, ,
, }为等比数列.
}为等比数列. 中,
中,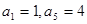 ,则
,则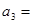 ( )
( )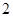
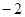
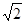
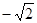
 ,从甲容器中取出
,从甲容器中取出 溶液,将其倒入乙容器中搅匀,再从乙容器中取出
溶液,将其倒入乙容器中搅匀,再从乙容器中取出 ,
, ,第
,第 次调和后的甲、乙两种溶液的浓度分别记为:
次调和后的甲、乙两种溶液的浓度分别记为: 、
、 .
. 分别表示
分别表示 ;
; .
. }中,a3=7,前3项之和S3=21, 则公比q的值为( )
}中,a3=7,前3项之和S3=21, 则公比q的值为( )
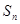 为等比数列
为等比数列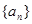 的前
的前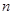 项和,且
项和,且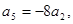 则
则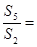 ( )
( )