题目内容
9.在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,垂足为D.(1)当点P在圆上运动时,线段PD的中点的轨迹C的方程;
(2)若M(x,y)是轨迹C上的动点,求x2-12y的最大值.
分析 (1)通过设C(x,y)可得P(x,2y),代入圆的方程计算即得结论;
(2)通过M(x,y)满足$\frac{{x}^{2}}{4}+{y}^{2}=1$,变形化简即得结论.
解答 解:(1)设C(x,y),则P(x,2y),
∵点P在圆上运动时,
∴x2+(2y)2=4,即$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)∵M(x,y)是轨迹C上的动点,
∴$\frac{{x}^{2}}{4}+{y}^{2}=1$,
∴x2+12y=4-4y2+12y,其中-1≤y≤1,
∴当y=1时,x2+12y有最大值12.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
13.函数y=f(x)图象如图所示,则函数的单调减区间为( )


| A. | [-3,3] | B. | [-1,2] | C. | [-3,-1] | D. | [2,3] |
1.椭圆$\frac{x^2}{4}+\frac{y^2}{m}=1$的焦距为2,则m的值为( )
| A. | 3 | B. | $\sqrt{15}$ | C. | 3或5 | D. | 3或$\sqrt{15}$ |
18.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左焦点为F,斜率为$\sqrt{3}$的直线过F与椭圆交于M、N两点,且$\overrightarrow{MF}=2\overrightarrow{FN}$,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{2}{3}$ |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,E为棱PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,E为棱PC的中点.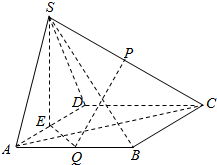 如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点. 已知过点M (2,1)的直线l和椭圆x2+4y2=36相交于点A、B,且线段AB恰好以M为中点,求直线l的方程和线段AB的长.
已知过点M (2,1)的直线l和椭圆x2+4y2=36相交于点A、B,且线段AB恰好以M为中点,求直线l的方程和线段AB的长.