题目内容
4.在平面直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=-2\sqrt{5}+\frac{\sqrt{2}}{2}t}\\{y=2\sqrt{5}+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为ρ=4cosθ.(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)将曲线C上的所有点的横坐标缩为原来的$\frac{1}{2}$倍,再将所得曲线向左平移1个单位,得到曲线C1,求曲线C1上的点到直线l放入距离的最小值.
分析 (1)曲线C的极坐标方程为ρ=4cosθ,化为ρ2=4ρcosθ,利用$\left\{\begin{array}{l}{{ρ}^{2}={x}^{2}+{y}^{2}}\\{x=ρcosθ}\end{array}\right.$,可得曲线C的直角坐标方程.直线l的参数方程为$\left\{\begin{array}{l}{x=-2\sqrt{5}+\frac{\sqrt{2}}{2}t}\\{y=2\sqrt{5}+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),两式相减可得:直线l的普通方程.
(2)将曲线C上的所有点的横坐标缩为原来的$\frac{1}{2}$倍,得(2x-2)2+y2=4,即${({x-1})^2}+\frac{y^2}{4}=1$.再将所得曲线向左平移1个单位,得C1:${x^2}+\frac{y^2}{4}=1$.设曲线C1上任一点P(cosθ,2sinθ),可得d=$\frac{|cosθ-2sinθ+4\sqrt{5}|}{\sqrt{2}}$,化简即可得出.
解答 解:(1)曲线C的极坐标方程为ρ=4cosθ,化为ρ2=4ρcosθ,可得曲线C的直角坐标方程为x2+y2=4x,即 (x-2)2+y2=4.
直线l的参数方程为$\left\{\begin{array}{l}{x=-2\sqrt{5}+\frac{\sqrt{2}}{2}t}\\{y=2\sqrt{5}+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),两式相减可得:直线l的普通方程为x-y+4$\sqrt{5}$=0.
(2)将曲线C上的所有点的横坐标缩为原来的$\frac{1}{2}$倍,得(2x-2)2+y2=4,
即${({x-1})^2}+\frac{y^2}{4}=1$.
再将所得曲线向左平移1个单位,得C1:${x^2}+\frac{y^2}{4}=1$.
又曲线C1的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=2sinθ\end{array}\right.$(θ为参数),设曲线C1上任一点P(cosθ,2sinθ),
则d=$\frac{{|cosθ-2sinθ+4\sqrt{5|}}}{{\sqrt{2}}}=\frac{{|4\sqrt{5}-\sqrt{5}sin(θ+ϕ)|}}{{\sqrt{2}}}≥\frac{{3\sqrt{10}}}{2}$.(其中$tanφ=-\frac{1}{2}$),
∴点P到直线l的距离的最小值为$\frac{{3\sqrt{10}}}{2}$.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、坐标变换、参数方程的应用、点到直线的距离公式、三角函数的单调性等基础知识与基本技能方法,考查了推理能力与计算能力,属于中档题.

| A. | 9和6 | B. | 6和$\frac{18}{5}$ | C. | 9和5 | D. | 9和$\frac{18}{5}$ |
| A. | (-1,2) | B. | (1,-2) | C. | (-2,4) | D. | (2,-4) |
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
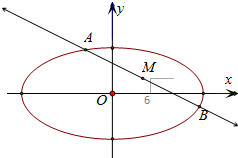 已知过点M (2,1)的直线l和椭圆x2+4y2=36相交于点A、B,且线段AB恰好以M为中点,求直线l的方程和线段AB的长.
已知过点M (2,1)的直线l和椭圆x2+4y2=36相交于点A、B,且线段AB恰好以M为中点,求直线l的方程和线段AB的长. 已知函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π.
已知函数f(x)=sin(ωx+$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π.