题目内容
15.对于任意实数x,记[x]表示不超过x的最大整数,{x}=x-[x],<x>表示不小于x的最小整数,若x1,x2,…xm(0≤x1<x2<…<xm≤n+1是区间[0,n+1]中满足方程[x]•{x}•<x>=1的一切实数,则x1+x2+…+xm的值是$\frac{n(n+1)}{2}$+$\frac{n}{n+1}$.分析 根据新定义,[x]表示不超过x的最大整数,{x}=x-[x],需要分类讨论,根据条件得到x═a+$\frac{1}{a(a+1)}$,继而求出a的可能值,最后代入计算即可.
解答 解:显然,x不可能是整数,
否则由于{x}=0,方程[x]•{x}•<x>=1不可能成立.
设[x]=a,则{x}=x-a,x=a+1,
代入得a(x-a)(a+1)=1,
解得x=a+$\frac{1}{a(a+1)}$.
考虑到x∈[0,n+1],且[x]≠0,所以a=1,2,3,4,5,…,n,
故符合条件的解有n个,即m=n,
则x1+x2+…+xm=x1+x2+…+xn=$\frac{n(n+1)}{2}$+1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=$\frac{n(n+1)}{2}$+1-$\frac{1}{n+1}$=$\frac{n(n+1)}{2}$+$\frac{n}{n+1}$.
故答案为:$\frac{n(n+1)}{2}$+$\frac{n}{n+1}$.
点评 本题考查了函数的值,需要分类进行讨论,新定义一般需要认真读题,理解题意,灵活利用已知定义,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
3.若复数$\frac{a+i}{2i}$的实部和虚部相等,则实数a等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
10.若复数Z满足$\overline Z$(1+i)=2i,则在复平面内Z对应的点的坐标是( )
| A. | (1,1) | B. | (1,-l) | C. | (-l,1) | D. | (-l,-l) |
20.已知I为全集,且B∩(∁IA)=B.求A∩B=( )
| A. | A | B. | B | C. | ∁IB | D. | ∅ |
4.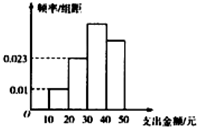 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
5.在等差数列{an}中,3(a3+a5)+2(a7+a10+a13)=24,则此数列前13项之和为( )
| A. | 126 | B. | 26 | C. | 13 | D. | 12 |