Question

【题目】某个公园有个池塘，其形状为直角△ABC，∠C=90°，AB=2百米，BC=1百米．

(1)现在准备养一批供游客观赏的鱼，分别在AB、BC、CA上取点D，E，F，如图(1)，使得EF‖AB，EF⊥ED，在△DEF喂食，求△DEF 面积S△DEF的最大值；

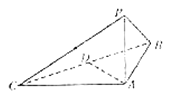
(2)现在准备新建造一个荷塘，分别在AB，BC，CA上取点D，E，F，如图(2)，建造△DEF

连廊（不考虑宽度）供游客休憩，且使△DEF为正三角形，求△DEF边长的最小值．

Answer 1

【答案】（1）；（2）百米．

【解析】

试题（1）求△DEF 面积S△DEF的最大值，先把△DEF 面积用一个参数表示出来，由于它是直角三角形，故只要求出两直角边DE和EF，直角△ABC中，可得，由于EF‖AB，EF⊥ED，那么有，因此我们可用CE来表示FE，DE．从而把S△DEF表示为CE的函数，然后利用函数的知识（或不等式知识）求出最大值；（2）．等边△DEF可由两边EF＝ED及确定，我们设，想办法也把与一个参数建立关系式，关键是选取什么为参数，由于等边△DEF位置不确定，我们可选取为参数，建立起与的关系．，则，中应用正弦定理可建立所需要的等量关系．

试题解析：（1）中，，百米，百米．

，可得，

，，

设，则米，

中，米，C到EF的距离米，

∵C到AB的距离为米，

∴点D到EF的距离为米，

可得，

∵，当且仅当时等号成立，

∴当时，即E为AB中点时，的最大值为． 7分

（2）设正的边长为，，

则，

设，可得

，，

∴．

在中，，

即，化简得， 12分

（其中是满足的锐角），

∴边长最小值为百米． 14分