题目内容
【题目】已知圆C经过M(![]() ,1),N(
,1),N(![]() ,1)两点,且圆心C在直线x+y﹣3=0上,过点A(﹣1,0)的动直线l与圆C相交于P、Q两点.
,1)两点,且圆心C在直线x+y﹣3=0上,过点A(﹣1,0)的动直线l与圆C相交于P、Q两点.
(Ⅰ)求圆C的方程;
(Ⅱ)当|PQ|=4![]() 时,求直线l的方程.
时,求直线l的方程.
【答案】(Ⅰ)x2+(y﹣3)2=9;(Ⅱ)x=﹣1或4x﹣3y+4=0.
【解析】
(Ⅰ)由题意知圆![]() 关于
关于![]() 轴对称,且圆心
轴对称,且圆心![]() 在直线
在直线![]() 上,由此求出圆心,再求出半径即可;
上,由此求出圆心,再求出半径即可;
(Ⅱ)讨论直线![]() 与
与![]() 轴垂直和
轴垂直和![]() 与
与![]() 轴不垂直时,分别求出满足条件的直线
轴不垂直时,分别求出满足条件的直线![]() 的方程即可.
的方程即可.
解:(Ⅰ)由圆![]() 经过
经过![]() ,
,![]() ,
,![]() ,
,![]() 两点,则圆
两点,则圆![]() 关于
关于![]() 轴对称;
轴对称;
设圆心![]() 为
为![]() ,由圆心
,由圆心![]() 在直线
在直线![]() 上,
上,
得![]() ,解得
,解得![]() ;
;
所以圆![]() 的半径为
的半径为![]() ,
,
所以圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)①当直线![]() 与
与![]() 轴垂直时,易知直线
轴垂直时,易知直线![]() 的方程为
的方程为![]() ,符合题意;
,符合题意;
②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
设![]() 的中点为
的中点为![]() ,由
,由![]() ,则
,则![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() ;
;
综上知,直线![]() 的方程为
的方程为![]() 或
或![]() .
.

【题目】社区服务是高中学生社会实践活动的一个重要内容,汉中某中学随机抽取了100名男生、100名女生,了解他们一年参加社区服务的时间,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
(单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
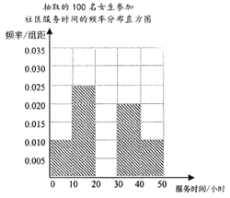
(1)完善男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
抽取的100名男生参加社区服务时间的频率分布表
社区服务时间 | 人数 | 频率 |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
合计 | 100 | 1 |
学生社区服务时间合格与性别的列联表
不合格的人数 | 合格的人数 | |
男 | ||
女 |
(2)按高中综合素质评价的要求,高中学生每年参加社区服务的时间不少于20个小时才为合格,根据上面的统计图表,完成抽取的这200名学生参加社区服务时间合格与性别的列联表,并判断是否有![]() 以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
(3)用以上这200名学生参加社区服务的时间估计全市9万名高中学生参加社区服务时间的情况,并以频率作为概率.
(i)求全市高中学生参加社区服务时间不少于30个小时的人数.
(ⅱ)对我市高中生参加社区服务的情况进行评价.
参考公式
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其
,其![]() )
)


