题目内容
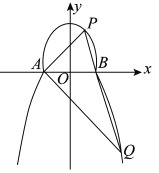
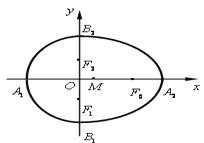
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,下顶点为
,下顶点为![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)利用![]() 表示出点
表示出点![]() 到直线
到直线![]() 的距离;再利用
的距离;再利用![]() 和
和![]() 的关系得到方程,求解得到标准方程;(2)当直线
的关系得到方程,求解得到标准方程;(2)当直线![]() 斜率存在时,假设直线方程,利用斜率之和为
斜率存在时,假设直线方程,利用斜率之和为![]() 得到
得到![]() 与
与![]() 的关系,将直线方程化为
的关系,将直线方程化为![]() ,从而得到定点;当斜率不存在时,发现直线也过该定点,从而求得结果.
,从而得到定点;当斜率不存在时,发现直线也过该定点,从而求得结果.
(1)解:由题意可知:直线![]() 的方程为
的方程为![]() ,即
,即![]()
则![]()
因为![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]()
又![]()
可解得![]() ,
,![]() ,
,![]()
所以椭圆![]() 的标准方程为
的标准方程为![]()
(2)证明:由(1)知![]()
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]()
代入![]() ,得
,得![]()
所以![]() ,即
,即![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
因为直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]()
所以![]()
![]()
整理得![]()
所以直线![]() 的方程为
的方程为![]()
显然直线![]() 经过定点
经过定点![]()
当直线![]() 的斜率不存在时,设直线
的斜率不存在时,设直线![]() 的方程为
的方程为![]()
因为直线![]() 与直线的斜率之和为
与直线的斜率之和为![]() ,设
,设![]() ,则
,则![]()
所以![]() ,解得
,解得![]()
此时直线![]() 的方程为
的方程为![]()
显然直线![]() 也经过该定点
也经过该定点![]()
综上,直线![]() 恒过点
恒过点![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】社区服务是高中学生社会实践活动的一个重要内容,汉中某中学随机抽取了100名男生、100名女生,了解他们一年参加社区服务的时间,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
(单位:小时)进行统计,得出男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
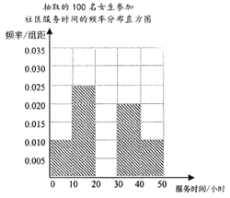
(1)完善男生参加社区服务时间的频率分布表和女生参加社区服务时间的频率分布直方图.
抽取的100名男生参加社区服务时间的频率分布表
社区服务时间 | 人数 | 频率 |
| 0.05 | |
| 20 | |
| 0.35 | |
| 30 | |
| ||
合计 | 100 | 1 |
学生社区服务时间合格与性别的列联表
不合格的人数 | 合格的人数 | |
男 | ||
女 |
(2)按高中综合素质评价的要求,高中学生每年参加社区服务的时间不少于20个小时才为合格,根据上面的统计图表,完成抽取的这200名学生参加社区服务时间合格与性别的列联表,并判断是否有![]() 以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
以上的把握认为参加社区服务时间达到合格程度与性别有关,并说明理由.
(3)用以上这200名学生参加社区服务的时间估计全市9万名高中学生参加社区服务时间的情况,并以频率作为概率.
(i)求全市高中学生参加社区服务时间不少于30个小时的人数.
(ⅱ)对我市高中生参加社区服务的情况进行评价.
参考公式
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.002 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其
,其![]() )
)
【题目】今年学雷锋日,某中学计划从高中三个年级选派4名教师和若干名学生去当学雷锋文明交通宣传志愿者,用分层抽样法从高中三个年级的相关人员中抽取若干人组成文明交通宣传小组,学生的选派情况如下:
年级 | 相关人数 | 抽取人数 |
高一 | 99 |
|
高二 | 27 |
|
高三 | 18 | 2 |
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)若从选派的高一、高二、高三年级学生中抽取3人参加文明交通宣传,求他们中恰好有1人是高三年级学生的概率;
(Ⅲ)若4名教师可去![]() 、
、![]() 、
、![]() 三个学雷锋文明交通宣传点进行文明交通宣传,其中每名教师去
三个学雷锋文明交通宣传点进行文明交通宣传,其中每名教师去![]() 、
、![]() 、
、![]() 三个文明交通宣传点是等可能的,且各位教师的选择相互独立.记到文明交通宣传点
三个文明交通宣传点是等可能的,且各位教师的选择相互独立.记到文明交通宣传点![]() 的人数为
的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
表![]()
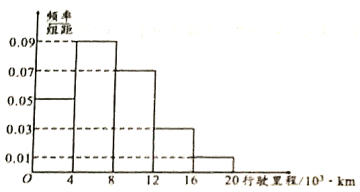
图![]()
(I)根据表![]() ,是否有
,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
(II)图![]() 给出的是
给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(III)用表![]() 中的频率估计概率,随机调查
中的频率估计概率,随机调查![]() 名
名![]() 岁以下车主,设其中购买了轿车的人数为
岁以下车主,设其中购买了轿车的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|