题目内容
【题目】已知点![]() 和椭圆
和椭圆![]() . 直线
. 直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .
.
(Ⅰ) 求椭圆![]() 的离心率;
的离心率;
(Ⅱ) 当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,当
,当![]() 为
为![]() 中点时,求
中点时,求![]() 的值 .
的值 .
【答案】(Ⅰ)![]() (Ⅱ)4(Ⅲ)
(Ⅱ)4(Ⅲ)![]()
【解析】
(Ⅰ)利用已知条件求出a,c,然后求解椭圆的离心率即可;
(Ⅱ)设P(x1,y1),Q(x2,y2),直线l的方程为![]() ,与椭圆联立,求出坐标,然后求解三角形的面积;
,与椭圆联立,求出坐标,然后求解三角形的面积;
(Ⅲ)法一:设点C(x3,y3),P(x1,y1),B(0,﹣2),结合椭圆方程求出P(x1,y1),然后求解斜率.
法二:设C(x3,y3),显然直线PB有斜率,设直线PB的方程为y=k1x﹣2,与椭圆联立,利用韦达定理求出P的坐标,求解斜率即可.
(Ⅰ)因为![]() ,所以
,所以![]()
所以离心率![]()
(Ⅱ)设![]()
若![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由 ,得
,得![]()
解得 ![]()
设![]() ,则
,则 ![]()
(Ⅲ)法一:
设点![]() ,
,
因为![]() ,
,![]() ,所以
,所以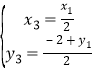
又点![]() ,
,![]() 都在椭圆上,
都在椭圆上,
所以
解得 或
或
所以 ![]() 或
或![]()
法二:
设![]()
显然直线![]() 有斜率,设直线
有斜率,设直线![]() 的方程为
的方程为![]()
由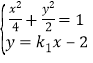 , 得
, 得 ![]()
所以
又![]()
解得 或
或 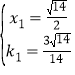
所以 或
或 
所以![]() 或
或![]()

【题目】为迎接![]() 年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核. 记
年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核. 记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了![]() 名学生的考核成绩,并作成如下茎叶图:
名学生的考核成绩,并作成如下茎叶图:
5 | 0 | 1 | 1 | 6 | ||||
6 | 0 | 1 | 4 | 3 | 3 | 5 | 8 | |
7 | 2 | 3 | 7 | 6 | 8 | 7 | 1 | 7 |
8 | 1 | 1 | 4 | 5 | 2 | 9 | ||
9 | 0 | 2 | 1 | 3 | 0 |
(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核成绩为优秀的概率;
(Ⅱ)从图中考核成绩满足![]() 的学生中任取
的学生中任取![]() 人,求至少有一人考核优秀的概率;
人,求至少有一人考核优秀的概率;
(Ⅲ)记![]() 表示学生的考核成绩在区间
表示学生的考核成绩在区间![]() 内的概率,根据以往培训数据,规定当
内的概率,根据以往培训数据,规定当![]() 时培训有效. 请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
时培训有效. 请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
【题目】2019年9月23日,在![]() 省
省![]() 市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量
市举办的2019年中国农民丰收节“新电商与农业科技创新”论坛上,来自政府相关部门的领导及11所中国高校的专家学者以“农业科技创新与乡村振兴”、“新农人与脱贫攻坚”为核心议题各抒己见,农产品方面的科技创新越来越成为21世纪大国崛起的一项重大突破.科学家对某农产品每日平均增重量![]() (单位:
(单位:![]() )与每日营养液注射量
)与每日营养液注射量![]() (单位:
(单位:![]() )之间的关系统计出表1一组数据:
)之间的关系统计出表1一组数据:
表1
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3.5 | 5 | 6.6 | 8.4 |
(1)根据表1和表2的相关统计值求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)计算拟合指数![]() 的值,并说明线性回归模型的拟合效果(
的值,并说明线性回归模型的拟合效果(![]() 的值在.98以上说明拟合程度好);
的值在.98以上说明拟合程度好);
(3)若某日该农产品的营养液注释量为![]() ,预测该日这种农产品的平均增长重量(结果精确到0.1).
,预测该日这种农产品的平均增长重量(结果精确到0.1).
附:①
表2
|
|
|
|
92.4 | 55 | 25 | 0.04 |
②对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: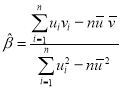 ,
,![]() ,
,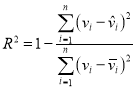 .
.