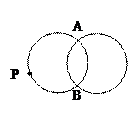题目内容
如图所示，已知动圆C与半径为2的圆F1外切，与半径为8的圆F2内切，且F1F2=6，
（1）求证：动圆圆心C的轨迹是椭圆；
（2）建立适当直角坐标系，求出该椭圆的方程。
（1）求证：动圆圆心C的轨迹是椭圆；
（2）建立适当直角坐标系，求出该椭圆的方程。
（1）同解析（2）椭圆的标准方程为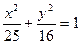
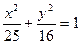
1）设动圆C的半径为r
依题意F1C=r+2
F2C=8－r
所以CF1+CF2=10>F1F2
所以圆心C的轨迹为椭圆
（2）以F1、F2所在直线为x轴，F1F2的中垂线为y轴建立直角坐标系
则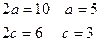
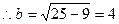
所以该椭圆的标准方程为…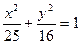
依题意F1C=r+2
F2C=8－r
所以CF1+CF2=10>F1F2
所以圆心C的轨迹为椭圆
（2）以F1、F2所在直线为x轴，F1F2的中垂线为y轴建立直角坐标系
则
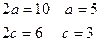
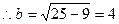
所以该椭圆的标准方程为
…
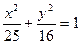练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
和圆
关于直线
对称，则直线
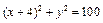相内切，且过点A（4，0），求这个动圆圆心的轨迹方程。
)2+(y+1)2=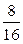
与圆(x－sinθ)2+(y－1)2=
(θ为锐角)的位置关( )
,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( ) 
