Question

【题目】（本小题满分14分）已知椭圆的左焦点为，右顶点为，点的坐标为，的面积为.

（I）求椭圆的离心率；

（II）设点在线段上，，延长线段与椭圆交于点，点，在轴上，，且直线与直线间的距离为，四边形的面积为.

（i）求直线的斜率；

（ii）求椭圆的方程.

Answer 1

【答案】（1） （2）（ⅰ） （ⅱ）

【解析】（Ⅰ）设椭圆的离心率为e.由已知，可得.又由，可得，即.又因为，解得.

所以，椭圆的离心率为

（Ⅱ）（ⅰ）依题意，设直线FP的方程为，则直线FP的斜率为.

由（Ⅰ）知，可得直线AE的方程为，即，与直线FP的方程联立，可解得，即点Q的坐标为.

由已知|FQ|=，有，整理得，所以，即直线FP的斜率为.

（ii）由，可得，故椭圆方程可以表示为.

由（i）得直线FP的方程为，与椭圆方程联立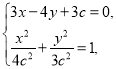消去，整理得，解得（舍去），或.因此可得点，进而可得，所以.由已知，线段的长即为与这两条平行直线间的距离，故直线和都垂直于直线.

因为，所以，所以的面积为，同理的面积等于，由四边形的面积为，得，整理得，又由，得.

所以，椭圆的方程为.