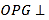题目内容
【题目】四面体ABCD中,AB和CD为对棱.设AB=a,CD=b,且异面直线AB与CD间的距离为d,夹角为θ.
(Ⅰ)若θ= ![]() ,且棱AB垂直于平面BCD,求四面体ABCD的体积;
,且棱AB垂直于平面BCD,求四面体ABCD的体积;
(Ⅱ)当θ= ![]() 时,证明:四面体ABCD的体积为一定值;
时,证明:四面体ABCD的体积为一定值;
(Ⅲ)求四面体ABCD的体积.
【答案】证明:(Ⅰ)如图5﹣2,由于棱AB⊥平面BCD,过B作CD边上的高BE,
则AB⊥BE,CD⊥BE,
故BE是异面直线AB与CD的距离,即d=BE.
所以VA﹣BCD= ![]() ABS△BCD=
ABS△BCD= ![]() a
a ![]() =
= ![]() abd.
abd.
(Ⅱ)如图5﹣3,过A作底面BCD的垂线,垂足为O,连结BO与CD相交于E.连结AE,
再过E作AB的垂线,垂足为F.
因为AB⊥CD,所以BO⊥CD(三垂线定理的逆定理),
所以CD⊥平面ABE,
因为EF平面ABE,
所以CD⊥EF,
又EF⊥AB.
所以EF即为异面直线AB,CD的公垂线.
所以EF=d.注意到CD⊥平面ABE.
所以VA﹣BCD= ![]() CDS△ABE=
CDS△ABE= ![]()
![]() ABEFCD=
ABEFCD= ![]() abd为定值.
abd为定值.
(Ⅲ)如图5﹣4:将四面体ABCD补成一个平行六面体ABB'D'﹣A'CC'D.
由于AB,CD所成角为θ,
所以∠DCA'=θ,
又异面直线AB与CD间的距离即上、下两底面AB',A'C'的距离,
所以VABB'D'﹣A'CC'D= ![]() absinθ×2d=abdsinθ.
absinθ×2d=abdsinθ.
显然VA﹣BCD= ![]() VABB'D'﹣A'CC'D=
VABB'D'﹣A'CC'D= ![]() abdsinθ
abdsinθ
【解析】(Ⅰ)根据异面直线的距离的定义结合三棱锥的体积公式进行求解即可.(Ⅱ)找出异面直线AB,CD的公垂线,结合三棱锥的体积公式进行证明即可.(Ⅲ)根据锥体的体积公式进行求解.

 名校课堂系列答案
名校课堂系列答案【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.