题目内容
【题目】一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的表面积是 . 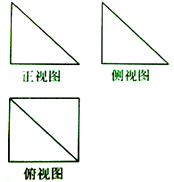
【答案】2+ ![]()
【解析】解:由三视图知几何体为一四棱锥,其直观图如图: 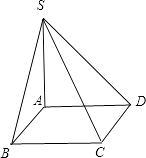
∵正视图和侧视图是腰长为1的两个全等的等腰直角三角形,∴四棱锥的底面是正方形,且边长为1,其中一条侧棱垂直于底面且侧棱长也为1,
∴四棱锥的四个侧面都为直角三角形,且SB=SD= ![]() ,
,
∴四棱锥的表面积S=S底面+S△SAB+S△SAD+S△SBC+S△SCD=1+2× ![]() ×1×1+2×
×1×1+2× ![]() ×1×
×1× ![]() =
= ![]() .
.
故答案是:2+ ![]() .
.
【考点精析】利用由三视图求面积、体积对题目进行判断即可得到答案,需要熟知求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积.

练习册系列答案
相关题目