题目内容
【题目】椭圆![]() 的焦距是
的焦距是![]() ,长轴长是短轴长3倍,任作斜率为
,长轴长是短轴长3倍,任作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(如图所示),且点
两点(如图所示),且点![]() 在直线
在直线![]() 的左上方.
的左上方.

(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)证明:![]() 的内切圆的圆心在一条定直线上。
的内切圆的圆心在一条定直线上。
【答案】(1)![]()
(2)![]()
(3)![]() 的内切圆的圆心在一条定直线
的内切圆的圆心在一条定直线![]() 上
上
【解析】
(1)由题意求出椭圆方程中的![]() ,得解;
,得解;
(2)分别利用弦长公式及点到直线的距离公式求出三角形的底与高,再利用三角形面积公式求解即可;
(3)先证明![]() ,从而可得
,从而可得![]() 的角平分线平行
的角平分线平行![]() 轴,从而可证
轴,从而可证![]() 的内切圆的圆心在一条定直线上.
的内切圆的圆心在一条定直线上.
解:(1)由题意知:![]() ,得
,得![]() ,又
,又![]() ,
,
所以![]() ,
,
故椭圆![]() 的方程为:
的方程为:![]() ;
;
(2)设直线![]() 的方程为:
的方程为:![]() ,代入椭圆方程可得:
,代入椭圆方程可得:![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]() ,
,
又![]() ,解得
,解得![]() 或
或![]() ,
,
由题意可得![]() ,
,
故![]() 所在直线方程为
所在直线方程为![]() ,即
,即![]() ,
,
所以点![]() 到直线
到直线![]() 的距离
的距离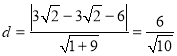 ,
,
故![]() 的面积为
的面积为![]() ;
;
(3)设直线![]() 的方程为:
的方程为:![]() ,代入椭圆方程可得:
,代入椭圆方程可得:![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
所以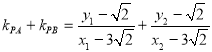 =
= ,
,
又![]()
![]()
![]()
![]()
![]() ,
,
即 ![]() ,所以
,所以![]() 的角平分线平行
的角平分线平行![]() 轴,
轴,
故![]() 的内切圆的圆心在一条定直线
的内切圆的圆心在一条定直线![]() 上.
上.

练习册系列答案
相关题目
【题目】某商场为改进服务质量,在进场购物的顾客中随机抽取了![]() 人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
人进行问卷调查.调查后,就顾客“购物体验”的满意度统计如下:
满意 | 不满意 | |
男 |
|
|
女 |
|
|
![]() 是否有
是否有![]() 的把握认为顾客购物体验的满意度与性别有关?
的把握认为顾客购物体验的满意度与性别有关?
![]() 若在购物体验满意的问卷顾客中按照性别分层抽取了
若在购物体验满意的问卷顾客中按照性别分层抽取了![]() 人发放价值
人发放价值![]() 元的购物券.若在获得了
元的购物券.若在获得了![]() 元购物券的
元购物券的![]() 人中随机抽取
人中随机抽取![]() 人赠其纪念品,求获得纪念品的
人赠其纪念品,求获得纪念品的![]() 人中仅有
人中仅有![]() 人是女顾客的概率.
人是女顾客的概率.
附表及公式: .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

