题目内容
【题目】已知![]() ,点
,点![]() 在第一象限,以
在第一象限,以![]() 为直径的圆与
为直径的圆与![]() 轴相切,动点
轴相切,动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若曲线![]() 在点
在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求满足
,求满足![]() 的点
的点![]() 的个数.
的个数.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)设![]() ,利用以
,利用以![]() 为直径的圆与
为直径的圆与![]() 轴相切列方程可得:
轴相切列方程可得:![]() ,整理可得:
,整理可得:![]() ,问题得解.
,问题得解.
(2)设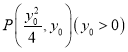 ,利用导数求得:
,利用导数求得:![]() ,结合
,结合![]() 及
及![]() 可得:
可得:![]() ,构造函数:
,构造函数:![]() 并利用导数知识可判断
并利用导数知识可判断![]() 在
在![]() 内有且只有两个零点,问题得解.
内有且只有两个零点,问题得解.
(1)设![]() ,
,
又![]() ,则
,则![]() 中点坐标为
中点坐标为![]() ,
,
因为以![]() 为直径的圆与
为直径的圆与![]() 轴相切,
轴相切,
所以![]() ,即
,即![]() ,
,
整理,得![]() 的方程为
的方程为![]() .
.
(2)由![]() ,得
,得![]() ,
,![]() ,
,
设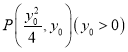 ,
,
则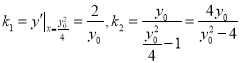 ,
,
由![]() ,即
,即![]() ,得
,得![]() (*),
(*),
令![]() ,
,
由![]() ,得
,得![]() ,或
,或![]() ,
,
因为当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
又![]() 的图象连续不断
的图象连续不断
所以![]() 在
在![]() 内有且只有两个零点,
内有且只有两个零点,
所以方程(*)有且只有两个不同的正根,
所以满足![]() 的点
的点![]() 的个数为2.
的个数为2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了使房价回归到收入可支撑的水平,让全体人民住有所居,近年来全国各一、二线城市打击投机购房,陆续出台了住房限购令.某市一小区为了进一步了解已购房民众对市政府岀台楼市限购令的认同情况,随机抽取了本小区50户住户进行调查,各户人平均月收入(单位:千元)的户数频率分布直方图如图,其中赞成限购的户数如下表:
人平均月收入 |
|
|
|
|
|
|
赞成户数 | 4 | 9 | 12 | 6 | 3 | 1 |
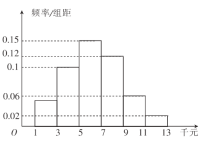
(1)若从人平均月收入在![]() 的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
的住户中再随机抽取两户,求所抽取的两户至少有一户赞成楼市限购令的概率;
(2)若将小区人平均月收入不低于7千元的住户称为“高收入户”,人平均月收入低于7千元的住户称为“非高收入户”根据已知条件完成如图所给的![]() 列联表,并说明能否有
列联表,并说明能否有![]() 的把握认为“收入的高低”与“赞成楼市限购令”有关.
的把握认为“收入的高低”与“赞成楼市限购令”有关.
非高收入户 | 高收入户 | ||
赞成 | |||
不赞成 | |||
总计 |
附:临界值表
| 0.1 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.63.5 | 10.828 |
参考公式: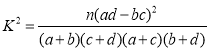 ,
,![]() .
.
