题目内容
若f（a+b）=f（a）•f（b），且f（1）=2，则
+
+…+
=______．
| f(2) |
| f(1) |
| f(3) |
| f(2) |
| f(2013) |
| f(2012) |
∵f（a+b）=f（a）•f（b），
∴
=f（a），
又f（1）=2，f（1+1）=f（1）•f（1），
∴
=f（1）=2，
同理可得，
=2，
=2，…，
=2，
∴
+
+…+
=2×（2012）=4024．
故答案为：4024．
∴
| f(a+b) |
| f(b) |
又f（1）=2，f（1+1）=f（1）•f（1），
∴
| f(2) |
| f(1) |
同理可得，
| f(3) |
| f(2) |
| f(4) |
| f(3) |
| f(2013) |
| f(2012) |
∴
| f(2) |
| f(1) |
| f(3) |
| f(2) |
| f(2013) |
| f(2012) |
故答案为：4024．
练习册系列答案
相关题目
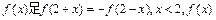单调递增，如果
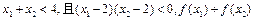的值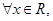
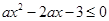恒成立”是真命题，则实数a的取值范围是 .
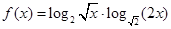的最小值为_________.