题目内容
如图所示,平面
 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, .
.
(1)求证
 平面
平面 ;(2)求平面
;(2)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.

 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, .
.(1)求证

 平面
平面 ;(2)求平面
;(2)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)证明见解析;(2)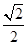 .
.
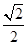 .
.试题分析:(方法一:传统几何方法)(1)证明线面平行,可在平面
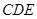 内找到一条线与面外的线AF平行即可,因此本小题可取CE中点为G,连接DG,FG,证明四边形AFGD为平行四边形即可完成证明;(2)本小题中可过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,把问题转化为证明
内找到一条线与面外的线AF平行即可,因此本小题可取CE中点为G,连接DG,FG,证明四边形AFGD为平行四边形即可完成证明;(2)本小题中可过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,把问题转化为证明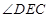 为平面
为平面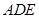 与平面
与平面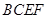 所成锐二面角的平面角,再利用直角三角形的边角关系算出其余弦值.
所成锐二面角的平面角,再利用直角三角形的边角关系算出其余弦值.(方法二:空间向量方法)(1)本小题可以以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立空间直角坐标系,把问题转化为证明AF的方向向量与平面CDE的一个法向量垂直(证它们的数量积为零),而根据题意易得这个法向量为
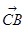 ;(2)本小题为常考的利用空间向量解决面面角问题,只需找到这两个面的法向量
;(2)本小题为常考的利用空间向量解决面面角问题,只需找到这两个面的法向量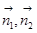 ,利用公式
,利用公式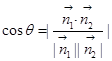 完成计算即可,但要注意本题面面角为锐二面角.
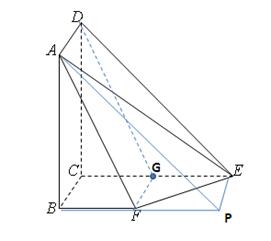
完成计算即可,但要注意本题面面角为锐二面角.试题解析:(方法一:)(1)取CE中点为G,连接DG,FG,
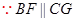 且
且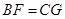 ,∴四边形BFGC为平行四边形,则
,∴四边形BFGC为平行四边形,则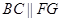 且
且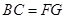 .
.∵四边形ABCD为矩形,∴
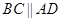 且
且 ,∴
,∴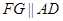 且
且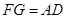 ,
,∴四边形AFGD为平行四边形,则
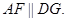
∵
 ,
, ,∴
,∴ .
.(2)过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,
∵
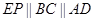 ,∴A,P,E,D四点共面.
,∴A,P,E,D四点共面.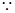 四边形
四边形 为直角梯形,四边形
为直角梯形,四边形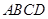 为矩形,
为矩形,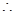
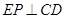 ,
,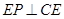 ,又
,又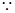
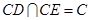 ,
,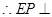 平面
平面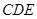 ,
,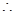
 ,又
,又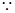 平面
平面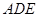
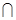 平面
平面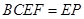 ,
,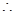
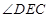 为平面
为平面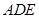 与平面
与平面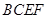 所成锐二面角的平面角.
所成锐二面角的平面角.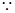
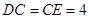 ,
,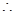
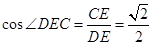 .即平面
.即平面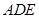 与平面
与平面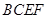 所成锐二面角的余弦值为
所成锐二面角的余弦值为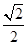 .
.(方法二:)(1)
 四边形
四边形 为直角梯形,四边形
为直角梯形,四边形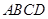 为矩形,
为矩形,
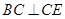 ,
,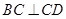 ,又
,又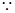 平面
平面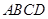
 平面
平面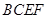 ,且平面
,且平面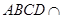 平面
平面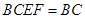 ,∴
,∴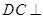 平面
平面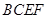 ,以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立如图所示空间直角坐标系.
,以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立如图所示空间直角坐标系.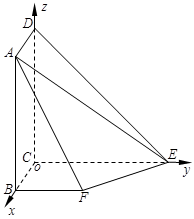
根据题意我们可得以下点的坐标:
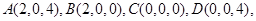
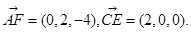
∵
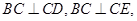 ∴
∴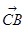 为平面
为平面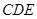 的一个法向量,又∵
的一个法向量,又∵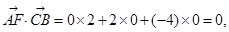
∴
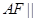 平面
平面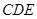 .
.(2)设平面
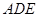 的一个法向量为
的一个法向量为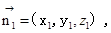 则
则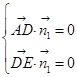 ,∵
,∵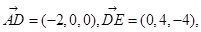
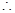
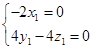 , 取
, 取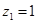 ,得
,得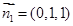 .
.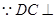 平面
平面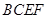 ,
,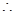 平面
平面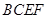 一个法向量为
一个法向量为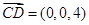 ,设平面
,设平面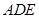 与平面
与平面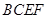 所成锐二面角的大小为
所成锐二面角的大小为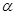 ,则
,则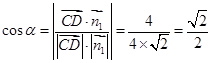 .因此,平面
.因此,平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为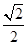 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
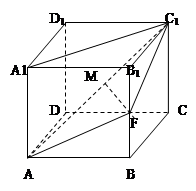
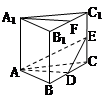
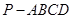 中,底面
中,底面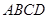 是平行四边形,
是平行四边形,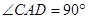 ,
,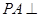 平面
平面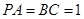 ,
,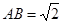 ,
,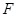 是
是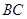 的中点.
的中点.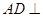 平面
平面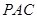 ;
; 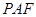 与平面
与平面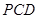 所成锐二面角的余弦值.
所成锐二面角的余弦值.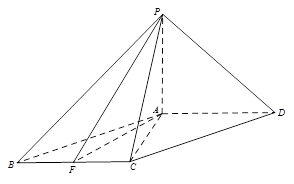
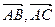 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量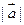 =
=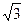 ,求向量
,求向量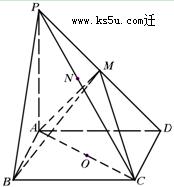
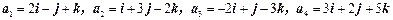 ,试问是否存在实数
,试问是否存在实数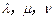 ,使
,使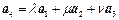 成立?如果存在,求出
成立?如果存在,求出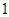 的正方体
的正方体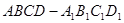 中,
中,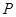 为线段
为线段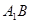 上的动点,则下列结论错误的是
上的动点,则下列结论错误的是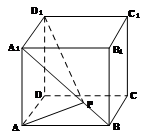
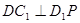
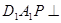 平面
平面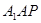
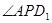 的最大值为
的最大值为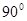
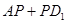 的最小值为
的最小值为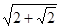
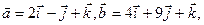 ,则这两个向量的位置关系是___________。
,则这两个向量的位置关系是___________。