题目内容
设函数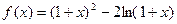
(1)求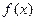 的单调增区间和单调减区间;
的单调增区间和单调减区间;
(2)若当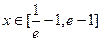 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式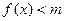 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)若关于x的方程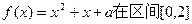 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。
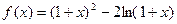
(1)求
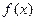 的单调增区间和单调减区间;
的单调增区间和单调减区间;(2)若当
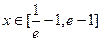 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式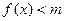 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;(3)若关于x的方程
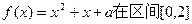 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。 (1)增区间:(0,+∞),减区间:(-1,0);(2) 时,
时,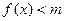 恒成立;(3)同解析。
恒成立;(3)同解析。
 时,
时,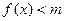 恒成立;(3)同解析。
恒成立;(3)同解析。(1)函数定义域为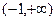
∵
由
∴增区间:(0,+∞),减区间:(-1,0)
(2)由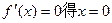

∵
∴
∴ 时,
时,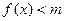 恒成立。
恒成立。
(3)

∵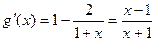 由
由
 ,
,
故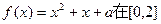 上恰有两相异实根
上恰有两相异实根
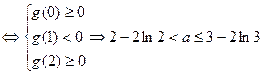
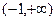
∵

由

∴增区间:(0,+∞),减区间:(-1,0)
(2)由
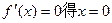

∵

∴

∴
 时,
时,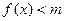 恒成立。
恒成立。(3)


∵
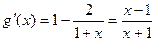 由
由
 ,
,故
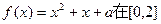 上恰有两相异实根
上恰有两相异实根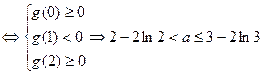

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=
,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=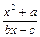 有且仅有两个不动点0和2.
有且仅有两个不动点0和2.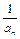 )=1,
)=1,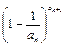 <
<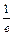 <
<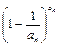 ;
;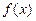 是定义在
是定义在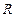 上的单调奇函数, 且
上的单调奇函数, 且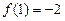 .
.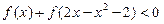 .
.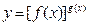 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得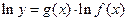 ,两边同时求导得
,两边同时求导得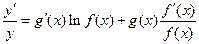 ,于是
,于是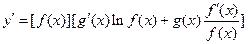 .运用此方法可以探求
.运用此方法可以探求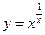 的一个单调递增区间是( )
的一个单调递增区间是( )
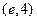
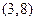
 满足对任意的
满足对任意的 都有
都有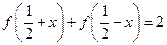 成立,则
成立,则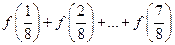 = .
= .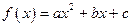 .
. 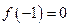 ,试判断函数
,试判断函数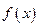 零点个数;
零点个数;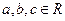 ,使
,使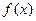 同时满足以下条件①对
同时满足以下条件①对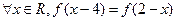 ,且
,且 ;②对
;②对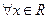 ,都有
,都有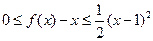 。若存在,求出
。若存在,求出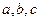 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。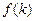 是满足不等式
是满足不等式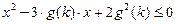 的自然数
的自然数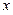 的个数,其中
的个数,其中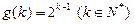 .
.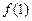 的值;
的值; ,令
,令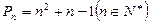 ,试比较
,试比较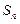 与
与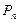 的大小.
的大小. ,例如:1
,例如:1 2=1,3
2=1,3 的值域为 .
的值域为 .