题目内容
已知函数 满足对任意的
满足对任意的 都有
都有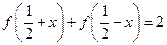 成立,则
成立,则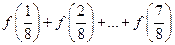 = .
= .
 满足对任意的
满足对任意的 都有
都有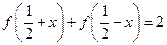 成立,则
成立,则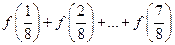 = .
= .7
提示:分别令x=0,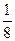 ,
,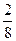 ,
,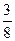 ,
,
由f(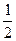 +x)+f(
+x)+f(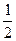 -x)=2,
-x)=2,
得f(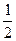 )+f(
)+f(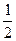 )=2,f(
)=2,f( )+f(
)+f(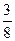 )=2,f(
)=2,f(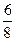 )+f(
)+f(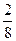 )=2,f(
)=2,f(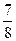 )+f(
)+f(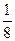 )=2,
)=2,
∴f(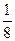 )+f(
)+f(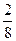 )+…+f(
)+…+f(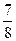 )=7
)=7
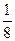 ,
,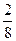 ,
,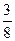 ,
,由f(
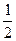 +x)+f(
+x)+f(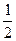 -x)=2,
-x)=2,得f(
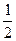 )+f(
)+f(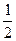 )=2,f(
)=2,f( )+f(
)+f(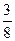 )=2,f(
)=2,f(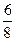 )+f(
)+f(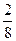 )=2,f(
)=2,f(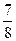 )+f(
)+f(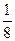 )=2,
)=2,∴f(
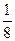 )+f(
)+f(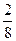 )+…+f(
)+…+f(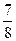 )=7
)=7
练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
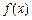 是定义在 [ – 1,1 ] 上的奇函数,且
是定义在 [ – 1,1 ] 上的奇函数,且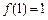 ,若m,
,若m,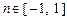 ,
,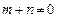 时有
时有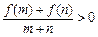 .
.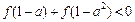 成立,求a的取值范围.
成立,求a的取值范围.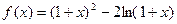
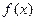 的单调增区间和单调减区间;
的单调增区间和单调减区间;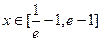 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式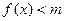 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;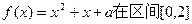 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。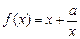 的定义域为
的定义域为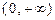 ,且
,且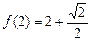 . 设点
. 设点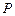 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点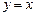 和
和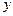 轴的垂线,垂足分别为
轴的垂线,垂足分别为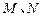 .
.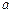 的值;
的值;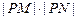 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;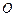 为坐标原点,求四边形
为坐标原点,求四边形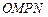 面积的最小值.
面积的最小值.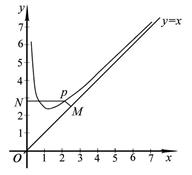
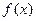 ,若存在闭区间
,若存在闭区间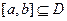 和常数
和常数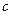 ,使得对任意
,使得对任意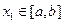 ,都有
,都有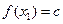 ,且对任意
,且对任意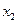 ∈D,当
∈D,当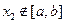 时,
时,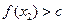 恒成立,则称函数
恒成立,则称函数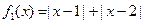 和
和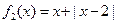 是否为R上的“平底型”函数? 并说明理由;
是否为R上的“平底型”函数? 并说明理由;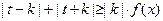 对一切
对一切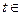 R恒成立,求实数
R恒成立,求实数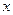 的取值范围;
的取值范围;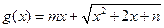 是区间
是区间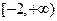 上的“平底型”函数,求
上的“平底型”函数,求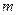 和
和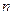 的值.
的值. 为偶函数且在区间
为偶函数且在区间 上是单调增函数.
上是单调增函数. 的解析式;
的解析式; ,若
,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
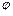 )(A>0,ω>0,|
)(A>0,ω>0,|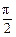 )图象的一部分,试求出其解析式.
)图象的一部分,试求出其解析式.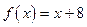 ,
,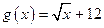 ,及任意的
,及任意的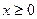 ,当甲公司投入
,当甲公司投入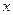 万元作宣传时,乙公司投入的宣传费若小于
万元作宣传时,乙公司投入的宣传费若小于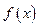 万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入
万元,则乙公司有失败的危险,否则无失败的危险;当乙公司投入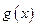 万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题:
万元,则甲公司有失败的危险,否则无失败的危险. 设甲公司投入宣传费x万元,乙公司投入宣传费y万元,建立如图直角坐标系,试回答以下问题: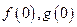 ;
;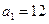 万元,乙在上述策略下,投入最少费用
万元,乙在上述策略下,投入最少费用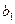 ;而甲根据乙的情况,调整宣传费为
;而甲根据乙的情况,调整宣传费为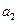 ;同样,乙再根据甲的情况,调整宣传费为
;同样,乙再根据甲的情况,调整宣传费为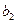
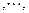 如此得当甲调整宣传费为
如此得当甲调整宣传费为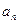 时,乙调整宣传费为
时,乙调整宣传费为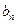 ;试问是否存在
;试问是否存在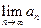 ,
,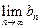 的值,若存在写出此极限值(不必证明),若不存在,说明理由.
的值,若存在写出此极限值(不必证明),若不存在,说明理由. 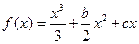 有两个极值点
有两个极值点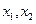 ,且满足:
,且满足: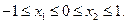
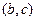 移动所形成的区域的面积;(Ⅱ)当
移动所形成的区域的面积;(Ⅱ)当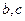 变化时,求
变化时,求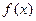 极大值的取值范围。
极大值的取值范围。