题目内容
幂指函数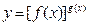 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得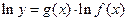 ,两边同时求导得
,两边同时求导得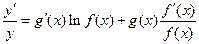 ,于是
,于是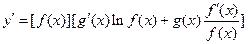 .运用此方法可以探求
.运用此方法可以探求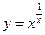 的一个单调递增区间是( )
的一个单调递增区间是( )
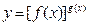 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得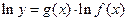 ,两边同时求导得
,两边同时求导得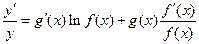 ,于是
,于是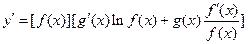 .运用此方法可以探求
.运用此方法可以探求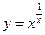 的一个单调递增区间是( )
的一个单调递增区间是( )A. | B.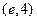 | C.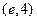 | D.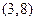 |
A
由题意可得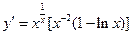 ,所以当
,所以当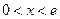 时,
时,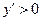 ,函数单调递增;当
,函数单调递增;当 时,
时,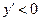 ,函数单调递减.综合可知函数的单调递增区间为
,函数单调递减.综合可知函数的单调递增区间为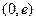 ,递减区间为
,递减区间为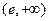 .注意到
.注意到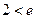 ,所以
,所以 是函数
是函数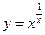 的一个单调递增区间.
的一个单调递增区间.
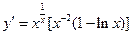 ,所以当
,所以当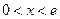 时,
时,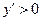 ,函数单调递增;当
,函数单调递增;当 时,
时,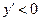 ,函数单调递减.综合可知函数的单调递增区间为
,函数单调递减.综合可知函数的单调递增区间为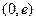 ,递减区间为
,递减区间为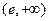 .注意到
.注意到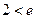 ,所以
,所以 是函数
是函数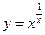 的一个单调递增区间.
的一个单调递增区间.
练习册系列答案
相关题目
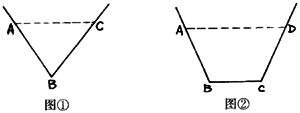
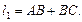
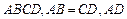 ∥
∥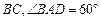 ,过水湿周
,过水湿周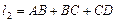 .若
.若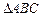 与梯形ABCD的面积都为S,
与梯形ABCD的面积都为S,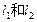 的最小值;
的最小值; 为常数,且
为常数,且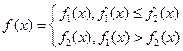 。
。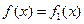 对所有的实数
对所有的实数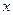 成立的充要条件(用
成立的充要条件(用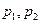 表示);
表示);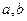 为两实数,
为两实数,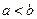 且
且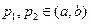 ,若
,若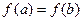 ,求证:
,求证: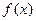 在区间
在区间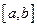 上的单调增区间的长度和为
上的单调增区间的长度和为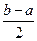 (闭区间
(闭区间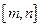 的长度定义为
的长度定义为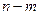 )。
)。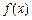 是定义在 [ – 1,1 ] 上的奇函数,且
是定义在 [ – 1,1 ] 上的奇函数,且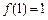 ,若m,
,若m,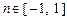 ,
,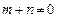 时有
时有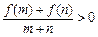 .
.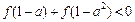 成立,求a的取值范围.
成立,求a的取值范围.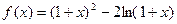
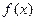 的单调增区间和单调减区间;
的单调增区间和单调减区间;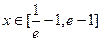 时(其中e=2.71828…),不等式
时(其中e=2.71828…),不等式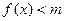 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;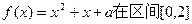 上恰有两个相异的实根,求实数a的取值范围。
上恰有两个相异的实根,求实数a的取值范围。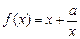 的定义域为
的定义域为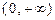 ,且
,且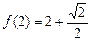 . 设点
. 设点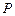 是函数图象上的任意一点,过点
是函数图象上的任意一点,过点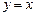 和
和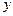 轴的垂线,垂足分别为
轴的垂线,垂足分别为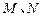 .
.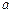 的值;
的值;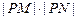 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由; 为坐标原点,求四边形
为坐标原点,求四边形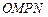 面积的最小值.
面积的最小值.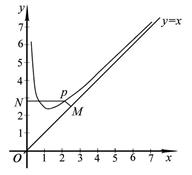
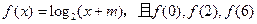 成等差数列.
成等差数列. 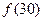 的值;
的值;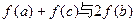 的大小关系,并证明你的结论.
的大小关系,并证明你的结论. 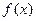 ,若存在闭区间
,若存在闭区间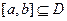 和常数
和常数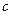 ,使得对任意
,使得对任意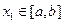 ,都有
,都有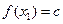 ,且对任意
,且对任意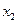 ∈D,当
∈D,当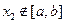 时,
时,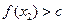 恒成立,则称函数
恒成立,则称函数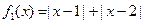 和
和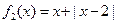 是否为R上的“平底型”函数? 并说明理由;
是否为R上的“平底型”函数? 并说明理由;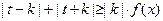 对一切
对一切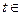 R恒成立,求实数
R恒成立,求实数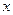 的取值范围;
的取值范围;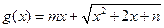 是区间
是区间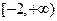 上的“平底型”函数,求
上的“平底型”函数,求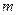 和
和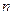 的值.
的值.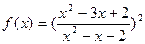 (其中
(其中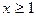 且
且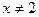 )
)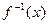
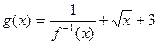 ,求函数g(x)最小值及相应的x值;
,求函数g(x)最小值及相应的x值;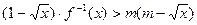 对于区间
对于区间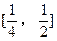 上的每一个x值都成立,求实数m的取值范围。
上的每一个x值都成立,求实数m的取值范围。