题目内容
【题目】下列命题中：
①已知点
，动点
满足
，则点的轨迹是一个圆；
②已知
，则动点的轨迹是双曲线；
③两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于1；
④在平面直角坐标系内，到点
和直线
的距离相等的点的轨迹是抛物线；
正确的命题是_________．
【答案】①③
【解析】
根据轨迹方程的求解，以及双曲线的定义，相关系数的性质，结合选项进行逐一分析即可.
①：设动点
，由
，故可得
，
整理得：
，且
，故该方程表示圆，则①正确；
②：根据双曲线的定义，
，
则动点
的轨迹只表示双曲线的左支，故②错误；
③：根据相关系数的性质，相关性越强，则相关系数的绝对值就越接近于1，故③正确；
④：因为点
在直线
上，
故满足题意的点的轨迹为过点且垂直于直线
的直线，故④错误.
故答案为：①③.
练习册系列答案
备战中考寒假系列答案
相关题目
【题目】某企业为了提高企业利润，从2014年至2018年每年都对生产环节的改进进行投资，投资金额
（单位：万元）与年利润增长量
（单位：万元）的数据如表：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
年利润增长量 | 6.0 | 7.0 | 9.0 | 11.0 | 12.0 |
（1）记
年利润增长量
投资金额，现从2014年至2018年这5年中抽出两年进行调查分析，求所抽两年都是
万元的概率；
（2）请用最小二乘法求出关于的回归直线方程；如果2019年该企业对生产环节改进的投资金额为10万元，试估计该企业在2019年的年利润增长量为多少？
参考公式：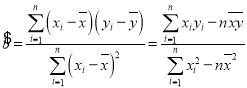
，
；
参考数据：
，
.
