��Ŀ����
����Ŀ��ij������ֲ��ԡ�һ�߶���Ԯ���͡���ѵ��Ͷ��ֱ�滮���£�2018�꣬�þ��ֲ��ڡ�һ�߶���Ԯ��Ͷ���ʽ�Ϊ16000��Ԫ������ѵ��Ͷ���ʽ�Ϊ1000��Ԫ.�ƻ�ÿ�ꡰһ�߶���Ԯ��Ͷ�����һ�����һ�룬����ѵ��Ͷ�����һ������һ��.
��1��������һ��þ��ֲ���һ�߶���Ԯ���͡���ѵ��Ͷ���ܺ�����?
��2����2018����������2018�����þ��ֲ�����һ�꿪ʼ��һ�߶���Ԯ���͡���ѵ����Ͷ��֮�Ͳ�����62000��Ԫ?����Ͷ����ָ����Ͷ��֮�ͣ�
���𰸡���1��2020�꣬Ͷ���ܺ����٣���2��2022�꿪ʼ����Ͷ��֮�Ͳ�����62000��.
��������
��1����2018���������n�ꡰһ�߶���Ԯ��Ͷ���ʽ�Ϊan������ѵ��Ͷ���ʽ�Ϊbn��Ͷ���ܺ�Ϊcn��д������{cn}��ͨ�ʽ�����û�������ʽ���ɵó����ۣ�
��2�����ݵȱ����е����ʽ�ó�ǰn�����Ͷ��֮�ͣ��в���ʽ���n���ɣ�
��1����2018���������n�ꡰһ�߶���Ԯ��Ͷ���ʽ�Ϊan��
����ѵ��Ͷ���ʽ�Ϊbn��Ͷ���ܺ�Ϊcn��
��{an}����16000Ϊ�����![]() Ϊ���ȵĵȱ����У�
Ϊ���ȵĵȱ����У�
{bn}����1000Ϊ�����2Ϊ���ȵĵȱ����У�
![]() ��
��![]() ��
��
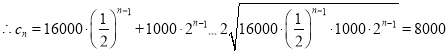 ��
��
���ҽ���![]() ����
����![]() ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�
����2020�꣬�þ��ֲ���һ�߶���Ԯ���͡���ѵ��Ͷ���ܺ����٣�
��2����{cn}��ǰ���ΪTn��
��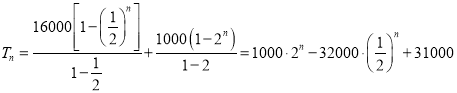 ��
��
��![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��![]() ����ȥ����
����ȥ����
��![]() ��
��![]() ��
��
���Դ�2018������ĵ�5�꼴2022�꿪ʼ����һ�߶���Ԯ���͡���ѵ����Ͷ��֮�Ͳ�����62000��.

 ��У����ϵ�д�
��У����ϵ�д�