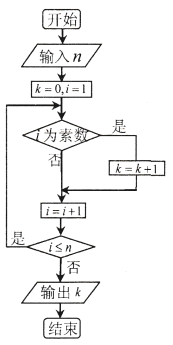
题目内容
【题目】某企业为了提高企业利润，从2014年至2018年每年都对生产环节的改进进行投资，投资金额
（单位：万元）与年利润增长量
（单位：万元）的数据如表：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
年利润增长量 | 6.0 | 7.0 | 9.0 | 11.0 | 12.0 |
（1）记
年利润增长量
投资金额，现从2014年至2018年这5年中抽出两年进行调查分析，求所抽两年都是
万元的概率；
（2）请用最小二乘法求出关于的回归直线方程；如果2019年该企业对生产环节改进的投资金额为10万元，试估计该企业在2019年的年利润增长量为多少？
参考公式：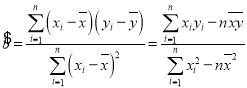
，
；
参考数据：
，
.
【答案】（1）
； （2）该企业在该年的年利润增长量大约为15.4万元.
【解析】
（1）利用列举法列举出
年中抽出两年的基本事件总数，然后求得其中两年都是
的基本事件数，根据古典概型概率计算公式，计算出所求的概率.
（2）利用回归直线方程计算公式，计算出回归直线方程，并将
代入回归直线方程，求得
年利润增长量的估计值.
（1）2014年至2018年的
分别记为：
，
，
，
，
，
抽取两年的基本事件有：
，
，
，
，
，
，
，
，
，
，共10种，
其中两年都是的基本事件有：，，，共3种，
故所求概率为
.
（2）
，
，
则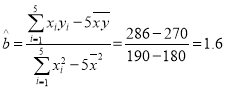
，
所以回归直线方程为
，将代入上述方程得
，
即该企业在该年的年利润增长量大约为15.4万元.
阅读快车系列答案
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y（万元）的几组对照数据:
x（年） | 2 | 3 | 4 | 5 | 6 |
y（万元） | 1 | 2.5 | 3 | 4 | 4.5 |
（1）若知道y对x呈线性相关关系，请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
（2）已知该工厂技术改造前该型号设备使用10年的维修费用为9万元，试根据（1）求出的线性回归方程，预测该型号设备技术改造后，使用10年的维修费用能否比技术改造前降低?参考公式: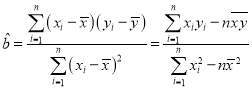
，
.
