题目内容
【题目】已知![]() 是奇函数
是奇函数![]() 的导函数,
的导函数,![]() ,当
,当![]() 时,
时,![]() ,则使得
,则使得![]() 成立的
成立的![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据条件构造函数g(x)![]() ,求函数导数,判断函数单调性和奇偶性,将不等式进行转化求解即可.
,求函数导数,判断函数单调性和奇偶性,将不等式进行转化求解即可.
设g(x)![]() ,则g′(x)=
,则g′(x)=![]() ,
,
∵当x>0时,xf′(x)﹣f(x)>0,
∴当x>0时,g′(x)>0,此时函数g(x)为增函数,
∵f(x)是奇函数,∴g(x)![]() 是偶函数,
是偶函数,
即当x<0时,g(x)为减函数.
∵f(﹣1)=0,∴g(﹣1)=g(1)=0,
当x>0时,f(x)>0等价为g(x)![]() >0,即g(x)>g(1),此时x>1,
>0,即g(x)>g(1),此时x>1,
当x<0时,f(x)>0等价为g(x)![]() <0,即g(x)<g(﹣1),此时﹣1<x<0,
<0,即g(x)<g(﹣1),此时﹣1<x<0,
综上不等式的解集为(﹣1,0)∪(1,+∞),
故选:A.

 寒假创新型自主学习第三学期寒假衔接系列答案
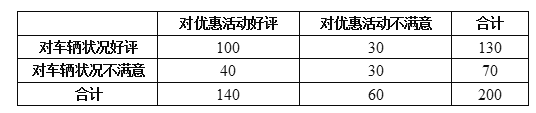
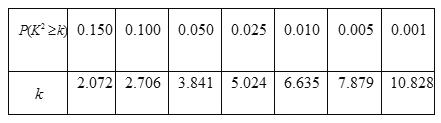
寒假创新型自主学习第三学期寒假衔接系列答案【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
【题目】光伏发电是将光能直接转变为电能的一种技术,具有资源的充足性及潜在的经济性等优点,在长期的能源战略中具有重要地位,2015年起,国家能源局、国务院扶贫办联合在6省的30个县开展光伏扶贫试点,在某县居民中随机抽取50户,统计其年用量得到以下统计表.以样本的频率作为概率.
用电量(单位:度) |
|
|
|
|
|
户数 | 7 | 8 | 15 | 13 | 7 |
(Ⅰ)在该县居民中随机抽取10户,记其中年用电量不超过600度的户数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(Ⅱ)在总结试点经验的基础上,将村级光伏电站稳定为光伏扶贫的主推方式.已知该县某自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组,该机组所发电量除保证该村正常用电外,剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1000度,试估计该机组每年所发电量除保证正常用电外还能为该村创造直接受益多少元?
【题目】某企业三月中旬生产A、B、C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
产品类别 | A | B | C |
产品数量(件) | 1 300 | ||
样本容量(件) | 130 |
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C的产品数量是( )
A.80B.800C.90D.900