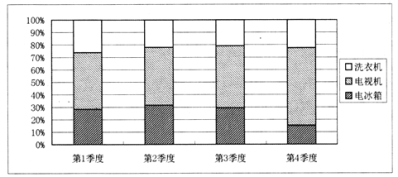
题目内容
【题目】如图所示,在长方体![]() 中,已知
中,已知![]() ,
,![]() .
.

(1)求:凸多面体![]() 的体积;
的体积;
(2)若![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)若点![]() 、
、![]() 分别在棱
分别在棱![]() 、
、![]() 上滑动,且线段
上滑动,且线段![]() 的长恒等于
的长恒等于![]() ,线段
,线段![]() 的中点为
的中点为![]()
①试证:点![]() 必落在过线段
必落在过线段![]() 的中点
的中点![]() 且平行于底面
且平行于底面![]() 的平面上;
的平面上;
②试求点![]() 的轨迹.
的轨迹.
【答案】(1)10;(2)![]() (3)①证明见解析;②点
(3)①证明见解析;②点![]() 的轨迹为以点M为圆心,
的轨迹为以点M为圆心,![]() 为半径的圆在长方体
为半径的圆在长方体![]() 内部的部分。
内部的部分。
【解析】
(1)根据多面体![]() 的体积是长方体
的体积是长方体![]() 的体积与三棱锥
的体积与三棱锥![]() 体积的差,可得解;
体积的差,可得解;
(2)由点M到平面![]() 的距离即为点
的距离即为点![]() 到平面
到平面![]() 的距离,即为点A到直线BD的距离,由三角形的等面积法可求解;
的距离,即为点A到直线BD的距离,由三角形的等面积法可求解;
(3)①由点P到底面ABCD的距离为定值![]() ,得点P必在过
,得点P必在过![]() 的中点M,且平行于底面ABCD的平面上;
的中点M,且平行于底面ABCD的平面上;
②由![]() ,
,![]() ,得点
,得点![]() 的轨迹为以点M为圆心,
的轨迹为以点M为圆心,![]() 为半径的圆在长方体
为半径的圆在长方体![]() 内部的部分。
内部的部分。
解:(1)因为多面体![]() 的体积是长方体
的体积是长方体![]() 的体积与三棱锥
的体积与三棱锥![]() 体积的差,
体积的差,
所以![]() ,
,
所以![]() ;
;
(2)因为点M到平面![]() 的距离即为点
的距离即为点![]() 到平面
到平面![]() 的距离,即为点A到直线BD的距离,
的距离,即为点A到直线BD的距离,
所以过A作![]() 交
交![]() 于N,则由三角形的等面积法得
于N,则由三角形的等面积法得![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
于是点M到平面![]() 的距离为
的距离为![]() ;
;
(3)①因为点P到底面ABCD的距离为定值![]() ,所以点P必在过
,所以点P必在过![]() 的中点M,
的中点M,
且平行于底面ABCD的平面上;
②连接EA,由于![]() ,
,![]() ,
,
所以点![]() 的轨迹为以点M为圆心,
的轨迹为以点M为圆心,![]() 为半径的圆在长方体
为半径的圆在长方体![]() 内部的部分。
内部的部分。
故得解.


练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目