题目内容
20.如图,输入正整数m,n,满足n≥m,则输出的p=$A_n^m$;
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算并输出变量P的值,模拟程序的运行,用表格对程序运行过程中各变量的值进行分析,不难得到输出结果.
解答 解:第一次循环:k=1,p=1,p=n-m+1;
第二次循环:k=2,p=(n-m+1)(n-m+2);
第三次循环:k=3,p=(n-m+1)(n-m+2)(n-m+3)
…
第m次循环:k=m,p=(n-m+1)(n-m+2)(n-m+3)…(n-1)n
此时结束循环,输出p=(n-m+1)(n-m+2)(n-m+3)…(n-1)n=Anm
故答案为:Anm.
点评 本题考查了循环结构的程序框图、排列公式,考查了学生的视图能力以及观察、推理的能力,要注意对第m次循环结果的归纳,这是本题的关键.

练习册系列答案
相关题目
15.已知一几何体的三视图如图所示,则该几何体的体积是( )
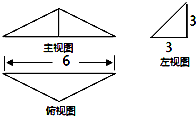

| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
5.若x∈R,那么$\frac{x}{x+1}$是正数的充要条件是( )
| A. | x>0 | B. | x<-1 | C. | x>0或x<-1 | D. | -1<x<0 |
9.某气象站观测点记录的连续4天里,AQI指数M与当天的空气水平可见度y(单位cm)的情况如下表1:
哈尔滨市某月AQI指数频数分布如下表2:
(1)设x=$\frac{M}{100}$,根据表1的数据,求出y关于x的回归方程;
(参考公式:$\hat y=\hat bx+\hat a$;其中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$,$\overline a=\overline y-\hat b\overline x$)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
| M | 900 | 700 | 300 | 100 |
| y | 0.5 | 3.5 | 6.5 | 9.5 |
| M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
(参考公式:$\hat y=\hat bx+\hat a$;其中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$,$\overline a=\overline y-\hat b\overline x$)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
10.若复数z=2-i ( i为虚数单位),则$\frac{10}{z}$=( )
| A. | 4+2i | B. | 20+10i | C. | 4-2i | D. | $\frac{20}{3}+\frac{10}{3}i$ |
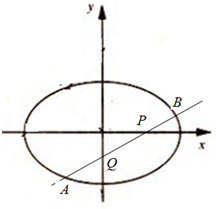 已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.