题目内容
已知直线经过点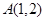 ,求分别满足下列条件的直线方程:
,求分别满足下列条件的直线方程:
(1)倾斜角的正弦为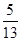 ;
;
(2)与两坐标轴的正半轴围成的三角形面积为4.
(1)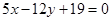 或
或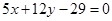 ;(2)
;(2)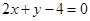
解析试题分析:(1)因为直线过定点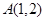 ,故只需求其斜率即可,由已知
,故只需求其斜率即可,由已知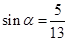 ,根据同角三角函数基本关系式,求
,根据同角三角函数基本关系式,求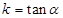 ,再用直线点斜式方程;(2)直线与与两坐标轴的正半轴围成的三角形面积与直线在坐标轴的截距有关,所以可设直线的截距式方程
,再用直线点斜式方程;(2)直线与与两坐标轴的正半轴围成的三角形面积与直线在坐标轴的截距有关,所以可设直线的截距式方程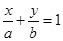
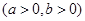 ,由面积为4,可得关于
,由面积为4,可得关于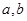 的方程,又直线过定点
的方程,又直线过定点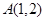 ,代入得关于
,代入得关于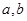 ,联立可求.
,联立可求.
试题解析:(1)设直线的倾斜角为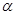 ,
,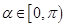 ,由
,由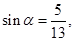 得
得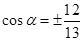 ,
,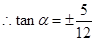 ,
,
当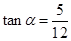 时,由点斜式方程得:
时,由点斜式方程得: 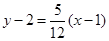 即
即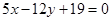 ;
;
当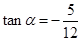 时,由点斜式方程得:
时,由点斜式方程得: 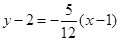 即
即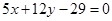 ,
,
综上:直线方程为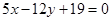 或
或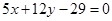 ;
;
(2)设直线在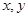 轴上的截距为
轴上的截距为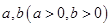 ,可设直线方程为
,可设直线方程为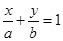 ,由题意得
,由题意得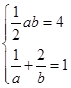 得
得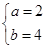 ,
,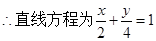 ,即:
,即: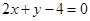 .
.
考点:1、直线的点斜式方程;2、直线的截距式方程.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
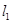 :
: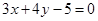 与直线
与直线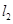 :
: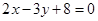 的交点
的交点 ,且满足下列条件的直线方程
,且满足下列条件的直线方程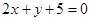 平行 ;
平行 ; 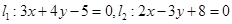 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程: 交于
交于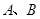 两点.
两点. 上的圆的方程.
上的圆的方程. 的直线的方程.
的直线的方程.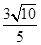 的直线方程.
的直线方程.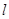 的参数方程为
的参数方程为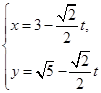 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为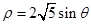 。
。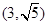 ,求|PA|+|PB|。
,求|PA|+|PB|。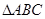 的三个顶点
的三个顶点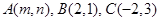 .
.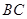 边所在直线方程;
边所在直线方程;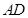 的方程为
的方程为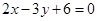 ,且
,且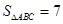 ,求
,求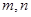 的值.
的值.