题目内容
求经过直线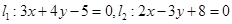 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程:
(1)与直线2x+3y+5=0平行; (2)与直线2x+3y+5=0垂直.
(1)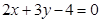 ;(2)
;(2)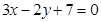
解析试题分析:根据题意先求出直线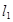 和
和 的交点
的交点 的坐标,根据两直线平行,则斜率相等,即可求出所求直线的方程;若两直线垂直,则斜率之积等于
的坐标,根据两直线平行,则斜率相等,即可求出所求直线的方程;若两直线垂直,则斜率之积等于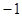 ,即可求出所求直线的方程.
,即可求出所求直线的方程.
试题解析: 由题意知:联立方程组 ,可得到两条直线的交点
,可得到两条直线的交点 的坐标为
的坐标为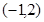 ,
,
因为所求直线与直线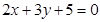 平行,可以设所求直线的方程为
平行,可以设所求直线的方程为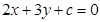 ,
,
因为过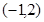 ,所以
,所以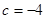 ,即所求直线的方程为
,即所求直线的方程为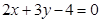 .
.
(2)设与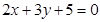 垂直的直线方程为
垂直的直线方程为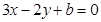 ,
,
因为过点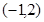 ,代入得
,代入得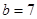 ,故所求直线方程为
,故所求直线方程为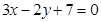 .
.
考点:本题考查了直线的方程,以及两条直线的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的三个顶点
的三个顶点 (4,0),
(4,0),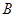 (8,10),
(8,10), (0,6).
(0,6).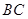 的直线方程;
的直线方程;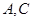 距离相等的直线方程。
距离相等的直线方程。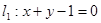 ,
,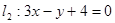 , 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
, 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.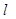 过点P(2,1),夹在两已知直线
过点P(2,1),夹在两已知直线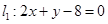 和
和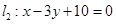 之间的线段AB恰被点P平分.
之间的线段AB恰被点P平分.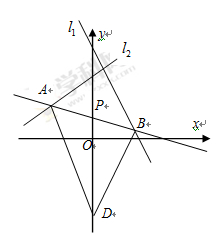
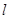 的方程;
的方程; ,求:
,求: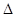 ABD的面积.
ABD的面积.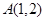 ,求分别满足下列条件的直线方程:
,求分别满足下列条件的直线方程: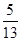 ;
;  中,以
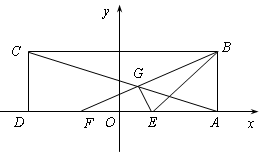
中,以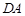 所在直线为
所在直线为 轴,以
轴,以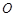 为坐标原点,建立如图所示的平面直角坐标系.已知点
为坐标原点,建立如图所示的平面直角坐标系.已知点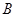 的坐标为
的坐标为 ,E、F为
,E、F为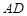 的两个三等分点,
的两个三等分点, 和
和 交于点
交于点 ,
, 的外接圆为⊙
的外接圆为⊙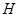 .
. 
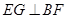 ;
;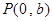 ,过点P作直线与⊙
,过点P作直线与⊙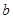 的取值范围.
的取值范围. 的切线
的切线 与两坐标轴交于点
与两坐标轴交于点
 .
.
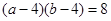 ;
;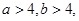 求△AOB的面积的最小值.
求△AOB的面积的最小值.