题目内容
已知圆 交于
交于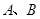 两点.
两点.
(1)求过A、B两点的直线方程;
(2)求过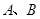 两点且圆心在直线
两点且圆心在直线 上的圆的方程.
上的圆的方程.
(1)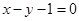 ;(2)
;(2)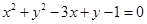
解析试题分析:(1)两个圆的方程相减,得直线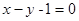 ,因为圆和圆的公共点为
,因为圆和圆的公共点为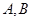 ,所以
,所以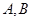 点的坐标满足方程
点的坐标满足方程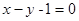 ,而两点只能确定一条直线,所以过
,而两点只能确定一条直线,所以过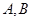 两点的直线方程为
两点的直线方程为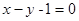 ,如果已知两个圆相切,那么相减得到的是公切线方程;(2)利用过两圆交点的直线系方程可设为
,如果已知两个圆相切,那么相减得到的是公切线方程;(2)利用过两圆交点的直线系方程可设为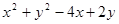
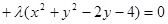
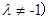 ,整理为圆的一般方程,进而求出圆心,再把圆心坐标
,整理为圆的一般方程,进而求出圆心,再把圆心坐标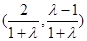 代入直线
代入直线 中,求
中,求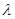 ,或者该题可以先求
,或者该题可以先求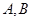 两点的坐标,在利用到圆心的距离相等列方程,求
两点的坐标,在利用到圆心的距离相等列方程,求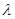 试题解析:(I)联立
试题解析:(I)联立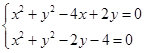 ,两式相减并整理得:
,两式相减并整理得: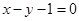
∴过A、B两点的直线方程为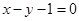 5分
5分
(II)依题意:设所求圆的方程为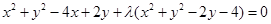 6分
6分
其圆心坐标为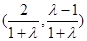 ,因为圆心在直线
,因为圆心在直线 上,所以
上,所以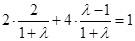 ,解得
,解得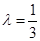
∴所求圆的方程为: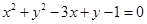 12分
12分
考点:1、直线的方程;2、圆的方程.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
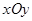 中,已知直线
中,已知直线 的斜率为
的斜率为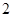 .
.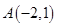 ,求直线
,求直线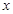 轴、
轴、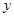 轴上的截距之和为
轴上的截距之和为 ,求直线
,求直线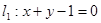 ,
,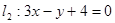 , 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
, 且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.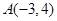 点射出,到
点射出,到 轴上的
轴上的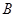 点后,被
点后,被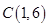 ,求
,求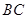 所在直线的方程及点
所在直线的方程及点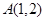 ,求分别满足下列条件的直线方程:
,求分别满足下列条件的直线方程: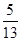 ;
; 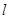 被两平行直线
被两平行直线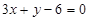
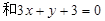 所截得的线段长为3,且直线过点(1,0),求直线
所截得的线段长为3,且直线过点(1,0),求直线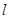 经过点
经过点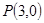 .
.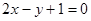 ,求直线
,求直线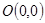 和点
和点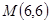 到直线
到直线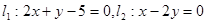
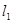 和直线
和直线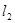 交点
交点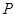 的坐标;
的坐标; 经过点
经过点