题目内容
已知函数f(x)=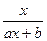 (a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
(a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
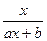 (a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
(a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.xn=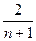 .
.
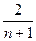 .
.由f(2)=1,得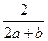 =1,即2a+b=2.
=1,即2a+b=2.
f(x)=x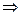
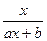 =x,即ax2+bx-x=0有唯一解.
=x,即ax2+bx-x=0有唯一解.
∵Δ=(b-1)2=0,∴b=1.
当x1=1时,xn=f(xn-1)=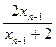 ,由已知有xn>0,
,由已知有xn>0,
则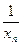 =
=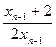 =
=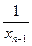 +
+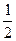 ,即
,即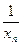 -
-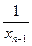 =
=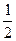 .
.
故{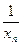 }是首项为1,公差为
}是首项为1,公差为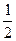 的等差数列.
的等差数列.
∴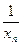 =1+
=1+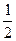 (n-1)=
(n-1)=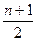 ,故xn=
,故xn=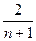 .
.
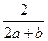 =1,即2a+b=2.
=1,即2a+b=2.f(x)=x
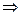
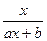 =x,即ax2+bx-x=0有唯一解.
=x,即ax2+bx-x=0有唯一解.∵Δ=(b-1)2=0,∴b=1.
当x1=1时,xn=f(xn-1)=
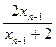 ,由已知有xn>0,
,由已知有xn>0,则
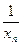 =
=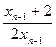 =
=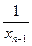 +
+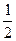 ,即
,即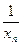 -
-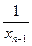 =
=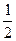 .
.故{
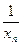 }是首项为1,公差为
}是首项为1,公差为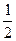 的等差数列.
的等差数列.∴
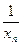 =1+
=1+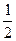 (n-1)=
(n-1)=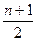 ,故xn=
,故xn=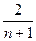 .
.
练习册系列答案
相关题目
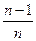
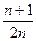
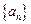 是公差为
是公差为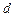 的等差数列,它的前
的等差数列,它的前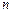 项和为
项和为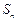 , 等比数列
, 等比数列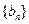 的前
的前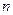 项和为
项和为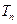 ,
,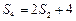 ,
,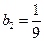 ,
,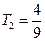
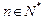 ,都有
,都有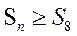 成立,求
成立,求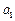 的取值范围
的取值范围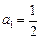 ,判别方程
,判别方程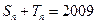 是否有解?说明理由
是否有解?说明理由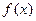 满足下列条件:
满足下列条件: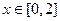 ,总有
,总有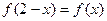 ,且
,且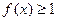 ,
,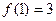 ;
;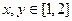 ,若
,若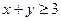 ,则
,则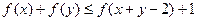 .
.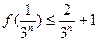 (
(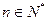 );(2)
);(2)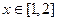 时,
时,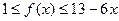 .
.