题目内容
设定义在[0,2]上的函数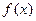 满足下列条件:
满足下列条件:
①对于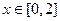 ,总有
,总有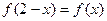 ,且
,且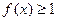 ,
,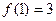 ;
;
②对于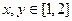 ,若
,若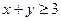 ,则
,则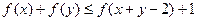 .
.
证明:(1)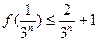 (
(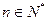 );(2)
);(2)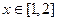 时,
时,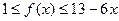 .
.
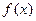 满足下列条件:
满足下列条件:①对于
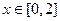 ,总有
,总有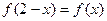 ,且
,且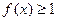 ,
,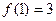 ;
;②对于
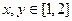 ,若
,若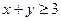 ,则
,则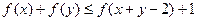 .
.证明:(1)
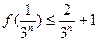 (
(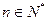 );(2)
);(2)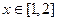 时,
时,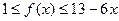 .
.证明略
由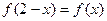 知,函数
知,函数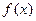 图像关于直线
图像关于直线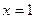 对称,则根据②可知:对于
对称,则根据②可知:对于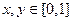 ,若
,若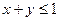 ,则
,则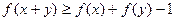 .……………2分
.……………2分
设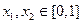 ,且
,且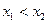 ,则
,则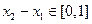 .
.
∵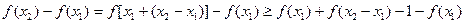
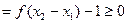 ,
,
∴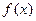 在[0,1]上是不减函数.………………………………………………4分
在[0,1]上是不减函数.………………………………………………4分
(1)∵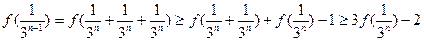 ,
,
∴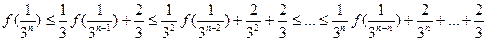
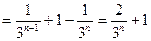 .…………………………………………………………8分
.…………………………………………………………8分
(2)对于任意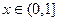 ,则必存在正整数
,则必存在正整数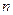 ,使得
,使得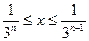 .
.
因为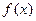 在(0,1)上是不减函数,所以
在(0,1)上是不减函数,所以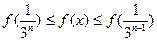 ,
,
由(1)知 .
.
由①可得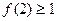 ,在②中,令
,在②中,令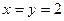 ,得
,得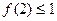 ,∴
,∴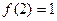 .
.
而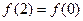 ,∴
,∴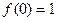 ,又
,又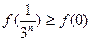 ,∴
,∴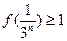 ,
,
∴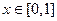 时,
时,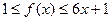 ..………………………………………12分
..………………………………………12分
∵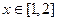 时,
时,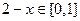 ,且
,且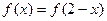 ,∴
,∴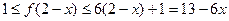 ,
,
因此,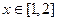 时,
时,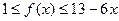 .…………………….………….14分
.…………………….………….14分
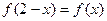 知,函数
知,函数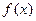 图像关于直线
图像关于直线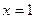 对称,则根据②可知:对于
对称,则根据②可知:对于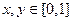 ,若
,若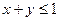 ,则
,则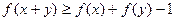 .……………2分
.……………2分设
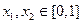 ,且
,且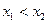 ,则
,则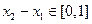 .
.∵
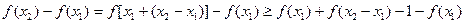
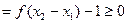 ,
,∴
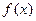 在[0,1]上是不减函数.………………………………………………4分
在[0,1]上是不减函数.………………………………………………4分(1)∵
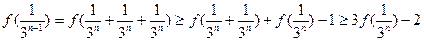 ,
,∴
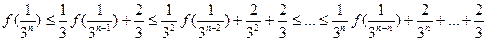
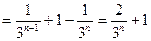 .…………………………………………………………8分
.…………………………………………………………8分(2)对于任意
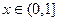 ,则必存在正整数
,则必存在正整数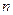 ,使得
,使得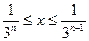 .
.因为
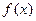 在(0,1)上是不减函数,所以
在(0,1)上是不减函数,所以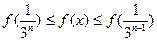 ,
,由(1)知
 .
. 由①可得
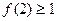 ,在②中,令
,在②中,令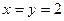 ,得
,得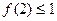 ,∴
,∴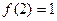 .
.而
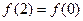 ,∴
,∴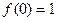 ,又
,又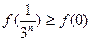 ,∴
,∴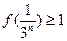 ,
,∴
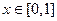 时,
时,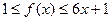 ..………………………………………12分
..………………………………………12分∵
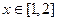 时,
时,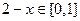 ,且
,且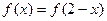 ,∴
,∴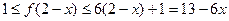 ,
,因此,
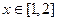 时,
时,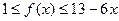 .…………………….………….14分
.…………………….………….14分
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
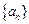 满足
满足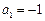 ,
,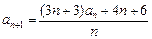 .(1)求
.(1)求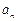 ;(2)令
;(2)令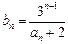 ,数列
,数列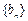 前
前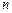 项和为
项和为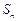 ,求证:当
,求证:当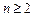 时,
时,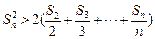 ;(3)证明:
;(3)证明: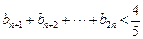 .
.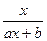 (a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
(a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.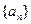 的通项公式为
的通项公式为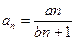 ,其中
,其中 为正数,判断数列
为正数,判断数列 是各项均为正数的等比数列,
是各项均为正数的等比数列, 是等比数列吗?为什么?
是等比数列吗?为什么?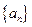 是等差数列,
是等差数列,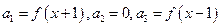 ,其中
,其中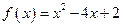 ,
,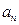 .
.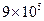 hm
hm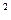 .地质工作者为了解这个地区沙漠面积的变化情况,从1998年开始进行了连续5年的观测,并在每年底将观测结果记录如下表:
.地质工作者为了解这个地区沙漠面积的变化情况,从1998年开始进行了连续5年的观测,并在每年底将观测结果记录如下表: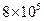 hm
hm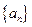 的前
的前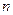 项和为
项和为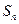 ,且
,且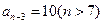 ,
,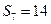 ,
,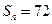 ,则
,则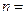 .
.