题目内容
已知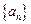 是公差为
是公差为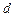 的等差数列,它的前
的等差数列,它的前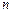 项和为
项和为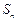 , 等比数列
, 等比数列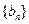 的前
的前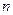 项和为
项和为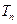 ,
,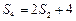 ,
,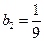 ,
,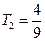
(1)求公差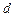 的值;
的值;
(2)若对任意的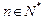 ,都有
,都有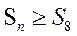 成立,求
成立,求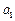 的取值范围
的取值范围
(3)若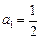 ,判别方程
,判别方程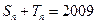 是否有解?说明理由
是否有解?说明理由
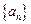 是公差为
是公差为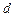 的等差数列,它的前
的等差数列,它的前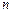 项和为
项和为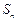 , 等比数列
, 等比数列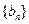 的前
的前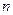 项和为
项和为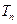 ,
,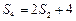 ,
,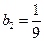 ,
,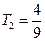
(1)求公差
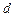 的值;
的值;(2)若对任意的
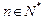 ,都有
,都有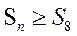 成立,求
成立,求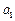 的取值范围
的取值范围(3)若
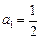 ,判别方程
,判别方程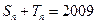 是否有解?说明理由
是否有解?说明理由(1)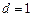 ;(2)
;(2)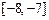 ;(3)方程
;(3)方程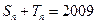 无解.
无解.
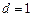 ;(2)
;(2)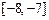 ;(3)方程
;(3)方程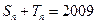 无解.
无解.解:(1)∵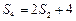 ,∴
,∴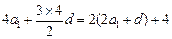 -------2分
-------2分
解得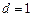 --------------------3分
--------------------3分
(2)解法1: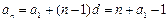 ------------4分
------------4分
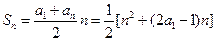
∵对任意的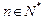 ,都有
,都有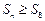 ,∴
,∴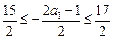
∴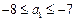
∴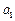 的取值范围是
的取值范围是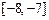 -----------8分
-----------8分
解法2:由于等差数列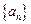 的公差
的公差
必须有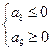 ,即
,即 ,求得
,求得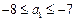
∴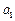 的取值范围是
的取值范围是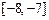
解法3:∵对任意的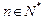 ,都有
,都有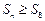 ,
,
所以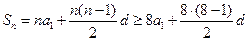
由于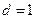 所以
所以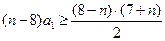
当 时
时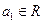
当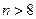 时
时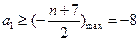
当 时
时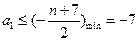
综合: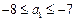
(3)由于等比数列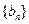 满足
满足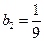 ,
,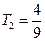
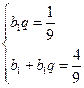 -------------------10分
-------------------10分
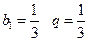

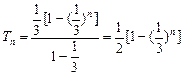
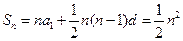 ---------12分
---------12分
则方程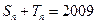 转化为:
转化为: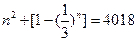
令: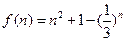 ,
,
由于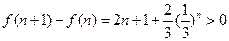
所以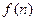 单调递增-
单调递增-
当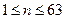 时,
时,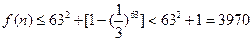
当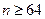 时,
时,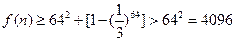
综合:方程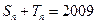 无解.---------16分
无解.---------16分
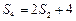 ,∴
,∴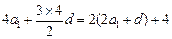 -------2分
-------2分解得
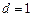 --------------------3分
--------------------3分(2)解法1:
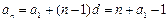 ------------4分
------------4分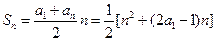
∵对任意的
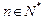 ,都有
,都有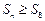 ,∴
,∴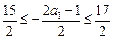
∴
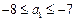
∴
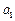 的取值范围是
的取值范围是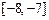 -----------8分
-----------8分解法2:由于等差数列
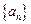 的公差
的公差
必须有
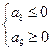 ,即
,即 ,求得
,求得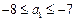
∴
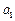 的取值范围是
的取值范围是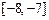
解法3:∵对任意的
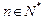 ,都有
,都有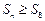 ,
,所以
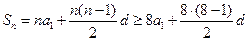
由于
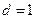 所以
所以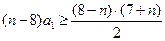
当
 时
时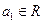
当
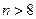 时
时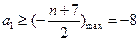
当
 时
时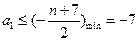
综合:
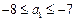
(3)由于等比数列
 满足
满足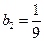 ,
,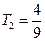
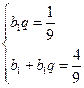 -------------------10分
-------------------10分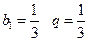

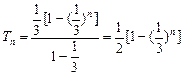
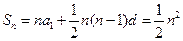 ---------12分
---------12分则方程
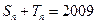 转化为:
转化为: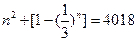
令:
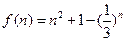 ,
,由于
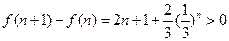
所以
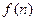 单调递增-
单调递增-当
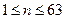 时,
时,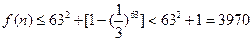
当
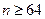 时,
时,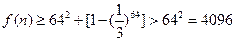
综合:方程
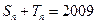 无解.---------16分
无解.---------16分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
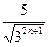 ,判断该数列是否为等差数列.
,判断该数列是否为等差数列.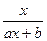 (a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn.
(a、b为常数,a≠0)满足f(2)=1,且f(x)=x有唯一解。如记xn=f(xn-1),且x1=1,n∈N*,求xn. ,问这个数列是等差数列吗?若是等差数列,其首项与公差分别是多少?
,问这个数列是等差数列吗?若是等差数列,其首项与公差分别是多少?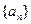 的通项公式为
的通项公式为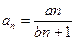 ,其中
,其中 为正数,判断数列
为正数,判断数列 是各项均为正数的等比数列,
是各项均为正数的等比数列, 是等比数列吗?为什么?
是等比数列吗?为什么?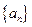 是等差数列,
是等差数列,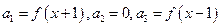 ,其中
,其中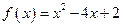 ,
,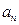 .
.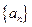 的通项公式为
的通项公式为 .
.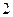 是否是数列
是否是数列 ,求
,求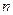 .
.