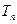题目内容
已知数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)当 时,证明不等式:
时,证明不等式: .
.
 满足
满足 .
.(1)求数列
 的通项公式;
的通项公式;(2)当
 时,证明不等式:
时,证明不等式: .
.(1)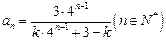 .
.
(2)证明见解析
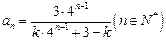 .
.(2)证明见解析
(1)当
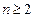 时,因为
时,因为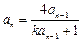 ,所以
,所以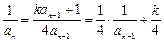 ,所以
,所以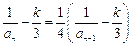 .因此:
.因此:① 当
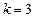 时,数列
时,数列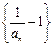 是各项为0的常数列,所以
是各项为0的常数列,所以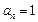 .
.② 当
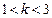 时,数列
时,数列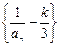 是以
是以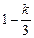 为首项,
为首项,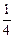 为公比的等比数列,所以
为公比的等比数列,所以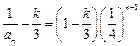 ,所以
,所以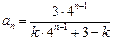 .又
.又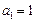 适合此式,因此
适合此式,因此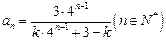 .
.综①②,得
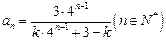 .
.(2)由
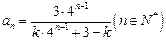 ,得
,得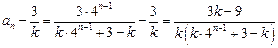 .
.因为
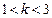 ,所以
,所以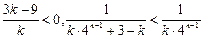 ,所以
,所以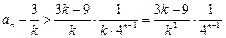 ,
,所以
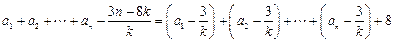
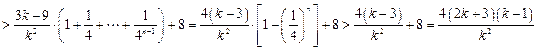 .
.因为
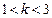 ,所以
,所以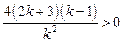 ,因此不等式
,因此不等式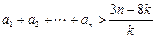 成立.
成立.
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 的前
的前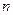 项和为
项和为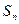 ,且满足
,且满足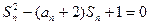 ,
,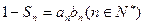 .
.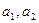 的值;
的值;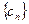 满足
满足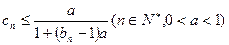 ,
,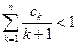 .
.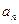 }的前n项和为
}的前n项和为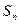 ,且
,且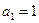 ,
,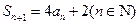 .
.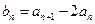 ,求证:数列{
,求证:数列{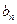 }是等比数列;
}是等比数列;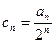 ,求证:数列{
,求证:数列{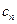 }是等差数列;
}是等差数列;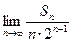 .
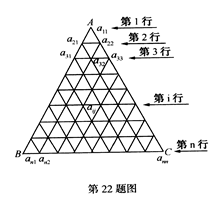
. ,…第i行中第j个数为a
,…第i行中第j个数为a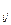 (1≤j≤i).若a
(1≤j≤i).若a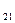 =
=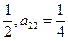
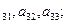
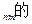 表达式(用含n,m的式子表示,不必证明);
表达式(用含n,m的式子表示,不必证明);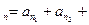 …+a
…+a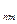 ,证明:n≤
,证明:n≤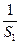 +
+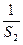 +…+
+…+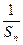 ≤
≤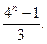

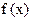 ,若存在
,若存在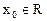 ,使
,使 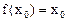 成立,则称
成立,则称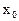 为
为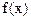 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = 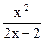 .
.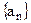 的各项均为负数,且满足
的各项均为负数,且满足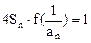 ,求数列
,求数列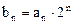 ,求
,求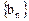 的前项和
的前项和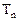 .
.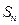 是等差数列
是等差数列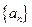 的前
的前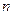 项和,且
项和,且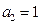 ,
,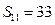 .
.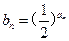 ,求证:数列
,求证:数列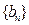 为等比数列,并求数列
为等比数列,并求数列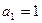 ,当
,当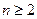 时,其前
时,其前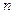 项和
项和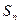 满足
满足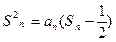
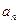 ;
;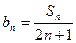 ,求数列{
,求数列{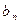 }的前项和
}的前项和