题目内容
已知数列{an}中a1=2,an+1=(-1)( an+2),n=1,2,3,….(Ⅰ)求{an}的通项公式;(Ⅱ)若数列{an}中b1=2,bn+1=,n=1,2,3,….证明:<bn≤a4n-3,n=1,2,3,…
(Ⅰ) an=[(-1)n+1] (Ⅱ)见解析
(Ⅰ)由题设:an+1=(-1)(an+2)=(-1)(an-)+(-1)(2+),
=(-1)(an-)+,∴an+1-=(-1)(an-).
所以,数列{an-}a是首项为2-,公比为-1)的等比数列,an-=(-1)n,
即an的通项公式为an=[(-1)n+1],n=1,2,3,….
(Ⅱ)用数学归纳法证明.
(ⅰ)当n=1时,因<2,b1=a1=2,所以<b1≤a1,结论成立.
(ⅱ)假设当n=k时,结论成立,即<bk≤a4k-3,,也即0<bn-≤a4k-3-,
当n=k+1时,bk+1-=-==>0,
又<=3-2,所以bk+1-=<(3-2)2(bk-)≤(-1)4(a4k-3-)=a4k+1-也就是说,当n=k+1时,结论成立.
根据(ⅰ)和(ⅱ)知<bn≤a4n-3,n=1,2,3,….
=(-1)(an-)+,∴an+1-=(-1)(an-).
所以,数列{an-}a是首项为2-,公比为-1)的等比数列,an-=(-1)n,
即an的通项公式为an=[(-1)n+1],n=1,2,3,….
(Ⅱ)用数学归纳法证明.
(ⅰ)当n=1时,因<2,b1=a1=2,所以<b1≤a1,结论成立.
(ⅱ)假设当n=k时,结论成立,即<bk≤a4k-3,,也即0<bn-≤a4k-3-,
当n=k+1时,bk+1-=-==>0,
又<=3-2,所以bk+1-=<(3-2)2(bk-)≤(-1)4(a4k-3-)=a4k+1-也就是说,当n=k+1时,结论成立.
根据(ⅰ)和(ⅱ)知<bn≤a4n-3,n=1,2,3,….

练习册系列答案
相关题目
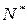 ),其中
),其中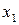 为正实数.
为正实数. 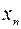 表示xn+1;
表示xn+1;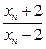 ,证明数列{
,证明数列{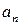 }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式; 满足
满足 .
. 时,证明不等式:
时,证明不等式: .
.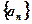 中,
中,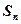 是其前
是其前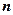 项和,
项和,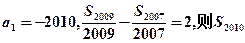 的值为
的值为  和正项等比数列
和正项等比数列 ,a7是b3和b7的等比中项.
,a7是b3和b7的等比中项. 的通项公式;
的通项公式; ,求数列{
,求数列{ }的前n项和Tn.
}的前n项和Tn.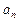 表示某企业第n年投入的治理污染的环保费用,用
表示某企业第n年投入的治理污染的环保费用,用 表示该企业第n年的产值. 设
表示该企业第n年的产值. 设 (万元)且以后治理污染的环保费用每年比上一年增加2
(万元)且以后治理污染的环保费用每年比上一年增加2 (万元);又设
(万元);又设 (万元),且企业的产值每年比上一年的平均增长率为10%. 用
(万元),且企业的产值每年比上一年的平均增长率为10%. 用 表示企业第n年 “对社会的有效贡献率”
表示企业第n年 “对社会的有效贡献率” 17
17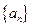 是由正数组成的数列,其前n项和为
是由正数组成的数列,其前n项和为 ,且满足关系:
,且满足关系:
 (2)求
(2)求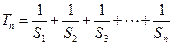
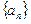 的公差为2,前
的公差为2,前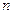 项和为
项和为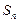 ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )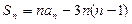
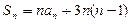
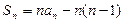
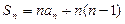
 }的前11项和为 ()
}的前11项和为 ()