题目内容
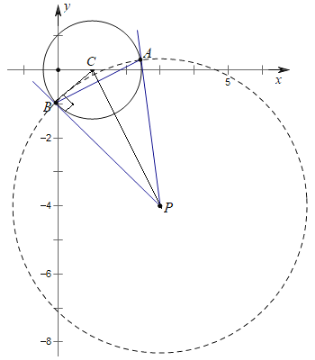
【题目】过点P(3,﹣4)作圆(x﹣1)2+y2＝2的切线，切点分别为A，B，则直线AB的方程为（ ）
A.x+2y﹣2＝0B.x﹣2y﹣1＝0C.x﹣2y﹣2＝0D.x+2y+2＝0
【答案】C
【解析】
画出图象，以P为圆心，以PB长度为半径可得到圆P，则圆(x﹣1)2+y2＝2与圆P的公共弦所在直线即为直线AB，利用两点间的距离公式和勾股定理可求出圆P的方程，然后两个方程相减即可得到直线AB的方程.
如图，圆P为以P为圆心，以PB长度为半径的圆，则圆(x﹣1)2+y2＝2与圆P的公共弦所在直线即为直线AB，
在
中，
，则
，
所以圆P的方程为：
，又圆C的方程为：(x﹣1)2+y2＝2，
以上两个等式相减可得，
，化简得，
.
故选：C.
练习册系列答案
相关题目
【题目】某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，统计结果如下表所示，已知这100位顾客中一次购物量超过7件的顾客占
.
一次购物量 | 1至3件 | 4至7件 | 8至11件 | 12至15件 | 16件及以上 |
顾客数（人） |
| 27 | 20 |
| 10 |
结算时间（ | 0.5 | 1 | 1.5 | 2 | 2.5 |
（1）确定
，
的值，并求顾客一次购物的结算时间的平均值；
（2）从收集的结算时间不超过
的顾客中，按分层抽样的方法抽取5人，再从这5人中随机抽取2人，求至少有1人的结算时间为
的概率.（注：将频率视为概率）
