题目内容
【题目】如图,三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
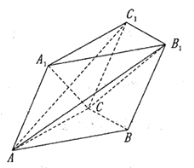
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的线面角为
所成的线面角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由平面ACC1A1⊥平面ABC,结合面面垂直的性质可得BC⊥A1C,再由B1C1∥BC,得A1C⊥平面AB1C1;(2)取AC中点M,连接A1M,由已知可得A1M⊥AC,且![]() ,令AA1=AC=2CB=2,则
,令AA1=AC=2CB=2,则![]() .以C为坐标原点,分别以CA,CB所在直线为x,y轴,过C且平行于A1M 的直线为z轴建立空间直角坐标系.分别求出平面ACB1 与平面A1B1C的一个法向量,由两法向量所成角的余弦值可得二面角C1﹣AB1﹣C的余弦值.
.以C为坐标原点,分别以CA,CB所在直线为x,y轴,过C且平行于A1M 的直线为z轴建立空间直角坐标系.分别求出平面ACB1 与平面A1B1C的一个法向量,由两法向量所成角的余弦值可得二面角C1﹣AB1﹣C的余弦值.
(1)因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() 是平行四边形,且
是平行四边形,且![]() ,所以
,所以![]() 是菱形,
是菱形,![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,因为
,因为![]() 是菱形,
是菱形,![]() ,
,
所以![]() 是正三角形,所以
是正三角形,所以![]() ,且
,且![]() .
.
令![]() ,则
,则![]() .
.
所以以![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则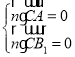 ,
,
所以 ,得
,得![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() .
.
由(1)知![]() 平面
平面![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
所以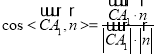
![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 名题金卷系列答案
名题金卷系列答案【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在![]() 内的概率;
内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?


