题目内容
13.已知a>b>c,则$\frac{1}{a-b}$+$\frac{1}{b-c}$+$\frac{4}{c-a}$的值是( )| A. | 非负数 | B. | 非正数 | C. | 正数 | D. | 不确定 |
分析 a>b>c,a-b>0,b-c>0,a-c>0.可得$\frac{a-c}{a-b}+\frac{a-c}{b-c}$=[(a-b)+(b-c)]$(\frac{1}{a-b}+\frac{1}{b-c})$,整理化简利用基本不等式的性质即可得出.
解答 解:∵a>b>c,a-b>0,b-c>0,a-c>0.
∴$\frac{a-c}{a-b}+\frac{a-c}{b-c}$=[(a-b)+(b-c)]$(\frac{1}{a-b}+\frac{1}{b-c})$=2+$\frac{b-c}{a-b}+\frac{a-b}{b-c}$≥2+2$\sqrt{\frac{b-c}{a-b}•\frac{a-b}{b-c}}$=4,
∴$\frac{1}{a-b}$+$\frac{1}{b-c}$≥$\frac{4}{a-c}$,
∴$\frac{1}{a-b}$+$\frac{1}{b-c}$+$\frac{4}{c-a}$≥0.
故选:A.
点评 本题考查了变形能力、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.某学生对一些对数进行运算,如图表格所示:
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是( )
| x | 0.21 | 0.27 | 1.5 | 2.8 |
| lgx | 2a+b+c-3(1) | 6a-3b-2(2) | 3a-b+c(3) | 1-2a+2b-c(4) |
| x | 3 | 5 | 6 | 7 |
| lgx | 2a-b(5) | a+c(6) | 1+a-b-c(7) | 2(a+c)(8) |
| x | 8 | 9 | 14 | |
| lgx | 3-3a-3c(9) | 4a-2b(10) | 1-a+2b(11) |
| A. | (3),(8) | B. | (4),(11) | C. | (1),(3) | D. | (1),(4) |
3.若复数$\frac{a+i}{2i}$的实部和虚部相等,则实数a等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
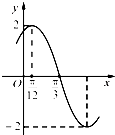 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )