题目内容
19.用逆矩阵的知识解方程MX=N,其中M=$|\begin{array}{l}{5}&{2}\\{4}&{1}\end{array}|$,N=$|\begin{array}{l}{5}\\{-8}\end{array}|$.分析 先求出M-1,利用X=M-1N计算即可.
解答 解:∵M=$[\begin{array}{l}{5}&{2}\\{4}&{1}\end{array}]$,设M-1=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$,
∴MM-1=$[\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}]$,即$[\begin{array}{l}{5}&{2}\\{4}&{1}\end{array}]$$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$=$[\begin{array}{l}{1}&{0}\\{0}&{1}\end{array}]$,
∴$\left\{\begin{array}{l}{5a+2c=1}\\{5b+2d=0}\\{4a+c=0}\\{4b+d=1}\end{array}\right.$,解得M-1=$[\begin{array}{l}{-\frac{1}{3}}&{\frac{2}{3}}\\{\frac{4}{3}}&{-\frac{5}{3}}\end{array}]$,
又∵N=$[\begin{array}{l}{5}\\{-8}\end{array}]$,MX=N,
∴X=M-1N=$[\begin{array}{l}{-\frac{1}{3}}&{\frac{2}{3}}\\{\frac{4}{3}}&{-\frac{5}{3}}\end{array}]$$[\begin{array}{l}{5}\\{-8}\end{array}]$=$[\begin{array}{l}{-7}\\{20}\end{array}]$.
点评 本题考查矩阵相关知识,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 540 | B. | 480 | C. | 360 | D. | 200 |
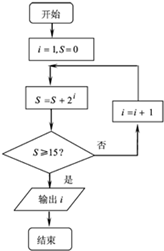
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | 1个 | B. | 2个 | C. | 无数多个 | D. | 1个或无数多个 |
| A. | 非负数 | B. | 非正数 | C. | 正数 | D. | 不确定 |
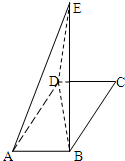 如图,在平行四边形ABCD中∠DAB=60°AB=2,AD=4,将△ABC沿BD折起到△EBD的位置.
如图,在平行四边形ABCD中∠DAB=60°AB=2,AD=4,将△ABC沿BD折起到△EBD的位置.